


極 值
a
變函數之極值的概念也可推廣到多變函數。
設有一函數 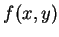 ,
, 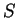 為一包含於
為一包含於  之定義域的集合。 對一
之定義域的集合。 對一
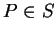 , 若
, 若
則稱  於
於 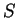 中, 在
中, 在  有絕對極大值
有絕對極大值 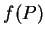 。 若存在一開球
。 若存在一開球
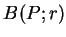 , 使得
, 使得
則稱  在
在  有一相對極大。 同理可定義絕對極小值及相對極小值。 相對極大值及相對極小值統稱相對極值。
有一相對極大。 同理可定義絕對極小值及相對極小值。 相對極大值及相對極小值統稱相對極值。
設 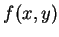 在平面上一封閉的區域連續, 則
在平面上一封閉的區域連續, 則  在此區域 中有絕對極大及絕對極小。為了簡便,
對相對極值, 我們常省略“相對” 二字, 而只稱極值。
在此區域 中有絕對極大及絕對極小。為了簡便,
對相對極值, 我們常省略“相對” 二字, 而只稱極值。
首先若 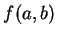 為
為  之一極大值, 則
之一極大值, 則  之圖形在平面上
之圖形在平面上 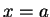 及
及
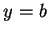 之 截域, 皆以
之 截域, 皆以
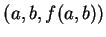 為極大點。 而若
為極大點。 而若 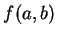 為
為  之一極小值, 則在前述二截距,
之一極小值, 則在前述二截距,
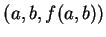 便為極小點。 故若
便為極小點。 故若  在
在 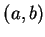 有一相對 極值, 且
有一相對 極值, 且  在
在 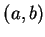 之一階偏導數皆存在, 則必有
之一階偏導數皆存在, 則必有
因此, 如我們所預料的, 在一極值發生處的切平面平行 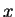 -
-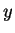 平面。 故欲求函數
平面。 故欲求函數  之極值,
先解同時滿足下二方程式之
之極值,
先解同時滿足下二方程式之 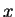 ,
, 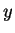 :
:
再檢驗每一組解是否為極大值或極小值。 當然, 如同單變數的情況,
極值也有可能 發生在邊界點, 或偏導數不存在處。 不過大部分我們遇到的例子中, 我們並不考慮這種情形。
例 1.設
 , 求
, 求  之極值。
之極值。 
例 2.令
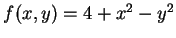 , 求
, 求  之極值。
之極值。 
對較複雜的例子, 由令一階偏導數為 0 之方程式解出的點,
並不易決定是否為極值, 此 情況對單變數也是類似。 因此我們也將給一以二階導數來檢驗極值的方法。
設
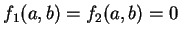 , 且二階偏導數
, 且二階偏導數 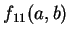 及
及
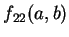 皆存在且不為 0。 若
皆存在且不為 0。 若  在
在 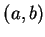 有極大, 則
有極大, 則
 之圖形在平面
之圖形在平面 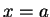 及
及 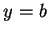 之 截距, 必皆為下凹, 且
之 截距, 必皆為下凹, 且
同理, 若  在
在 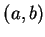 有極小, 則必有
有極小, 則必有
而若 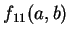 與
與 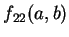 符號相反, 則
符號相反, 則  在
在 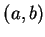 無極值。
我們敘述此結果如下,
此即兩變數之二階導數極值判定法。
無極值。
我們敘述此結果如下,
此即兩變數之二階導數極值判定法。
a
a
若 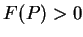 , 則
, 則
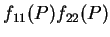 必為正, 因此
必為正, 因此  與
與
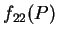 須同號。 故定理
1 之 (i) 及 (ii) 中的
須同號。 故定理
1 之 (i) 及 (ii) 中的  皆可以
皆可以 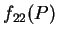 取代。
取代。
例 3.令
求  之極值。
之極值。

例 4.令
 , 求
, 求  之極值。
之極值。

例 5.令
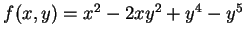 , 求
, 求  之極值。
之極值。

例 6.令
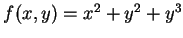 , 求
, 求  之極值。
之極值。

例 7.設長方體之三邊長之和固定, 試決定各邊長使其體積最大。

其次我們來看有限制的極值的問題, 並介紹
Lagrange 乘數法 。
我們先看底下兩個例子。 第一例為, 給定一不通過原點之曲面 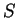 ,
找出
,
找出 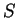 上最接近原點者。 第二例為, 令
上最接近原點者。 第二例為, 令 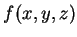 表在點
表在點 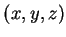 之溫度, 給定一三維空間中的曲線
之溫度, 給定一三維空間中的曲線 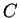 ,
求在此曲線上溫度最高及最低點。
,
求在此曲線上溫度最高及最低點。
上二例的一般形式為: 決定一多變函數
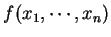 之極值,
其中
之極值,
其中
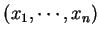 限制在
限制在  之定義域的一子集。 在第一例中, 即要求函數
之定義域的一子集。 在第一例中, 即要求函數  ,
, 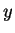 ,
, 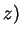
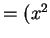
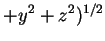 之極小值, 其中
之極小值, 其中 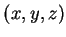 限制在某一給定 的曲面
限制在某一給定 的曲面 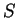 上。 在第二例中, 所限制的集合為一曲線。
上。 在第二例中, 所限制的集合為一曲線。
這類有限制的極值問題, 一般來說並不容易解,
此因並無一通則可解出所有問題。
當受限制的集合有極簡單的結構,
例如, 前二例中的一曲面或一曲線, 則有特殊的方法適用。 這就是所謂
Lagrange 乘數法。 我們先描述此方法的一般形式,
然後再以幾何的討論, 來說明此法行得通。
Lagrange 乘數法: 設有一函數
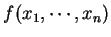 , 則在
, 則在
|
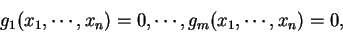
|
(7.2)
|
其中  , 之限制下, 使
, 之限制下, 使  有相對極值的點須滿足
有相對極值的點須滿足
|
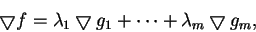
|
(7.3)
|
其中
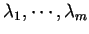 為常數。
為常數。
欲決定極值, 我們考慮由 (7.2) 中的 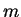 個限制方程式及 (7.3) 中的
個限制方程式及 (7.3) 中的
 個方程式, 總共
個方程式, 總共 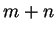 個方程式。 設法解出
個方程式。 設法解出 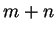 個未知數
個未知數
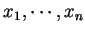 及
及
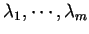 。
其中解出的
。
其中解出的
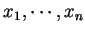 便有可能是
便有可能是  之極值。 在解的過程中, 我們藉助
之極值。 在解的過程中, 我們藉助
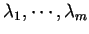 , 此
, 此 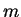 個數值解稱為 Lagrange 乘數。 每一個限制式均需要一個乘數。 函數
個數值解稱為 Lagrange 乘數。 每一個限制式均需要一個乘數。 函數  及
及
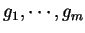 均設為可微。 此法只有限制式的數目
均設為可微。 此法只有限制式的數目 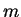 小於變數個數
小於變數個數
 , 且並非所有限制函數
, 且並非所有限制函數
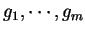 , 對
, 對
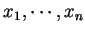 中的任意
中的任意 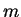 個 在極值處的 Jacobian皆為 0 才有效。 底下我們以幾何的討論來說明此法為何成立。
個 在極值處的 Jacobian皆為 0 才有效。 底下我們以幾何的討論來說明此法為何成立。
在前述第一例中, 我們欲決定在一給定的曲面 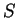 中, 最接近原點者。 而三維空間中一點
中, 最接近原點者。 而三維空間中一點 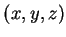 距原點之距離為
距原點之距離為 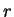 ,
若且唯若它落在半徑為
,
若且唯若它落在半徑為 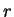 的球上, 即
的球上, 即
在此, 對一給定的 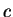 ,
,
稱為函數  之一等位面 。 球面
之一等位面 。 球面
 , 即為函數
, 即為函數 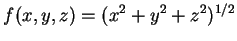 之一等位面。 我們便是要求
之一等位面。 我們便是要求  之極小值。
之極小值。
若由 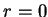 出發, 逐漸讓
出發, 逐漸讓 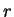 增大,
直到等位面第一次接觸到所給的曲面
增大,
直到等位面第一次接觸到所給的曲面 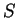 , 則每一接觸點, 皆為
, 則每一接觸點, 皆為 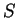 上最接近原點者。 欲決定那些接觸點的座標, 我們假設
上最接近原點者。 欲決定那些接觸點的座標, 我們假設 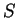 為由一些方程式
為由一些方程式 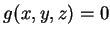 所描述。 若在每一接觸點
所描述。 若在每一接觸點 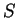 皆有切平面, 此切平面亦必為接觸點的 等位面的切平面。 因此,
在一接觸點, 曲面
皆有切平面, 此切平面亦必為接觸點的 等位面的切平面。 因此,
在一接觸點, 曲面 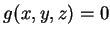 之梯度向量
之梯度向量
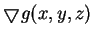 ,
與等位面
,
與等位面 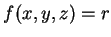 之梯度向量必須平行。 因此存在一常數
之梯度向量必須平行。 因此存在一常數
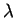 , 使得在每一接觸點
, 使得在每一接觸點
此即有一限制式下的 Lagrange 方法中的 (7.3) 式。
接著來看前述的第二例。 我們想在一給定的曲線 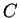 上找溫度函數
上找溫度函數
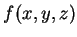 之 極值。 若將曲線
之 極值。 若將曲線 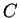 視為二曲面
視為二曲面
之交集, 則我們有一在二限制式下的極值問題。 二梯度向量
 及
及
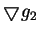 分別為上述二曲面之法向量, 故亦為交集曲線
分別為上述二曲面之法向量, 故亦為交集曲線 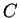 之法向量。 稍後我們證明溫度函數
之法向量。 稍後我們證明溫度函數  之 梯度向量
之 梯度向量
 ,
在極值處亦為
,
在極值處亦為 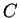 之法向量。 故
之法向量。 故
 與
與
 及
及
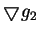 在同一平面上。 故若
在同一平面上。 故若
 及
及
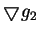 為二獨立向量, 則
為二獨立向量, 則
 可表示為
可表示為
 及
及
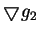 之線性組合, 即
之線性組合, 即
此即有二限制式下的 (7.3) 式。
欲證
 在極值處為
在極值處為 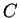 之法向量, 設
之法向量, 設 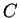 為一向量值函數
為一向量值函數
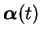 所描述, 其中
所描述, 其中 ![$t\in [a, b]$](img158.gif) 。 在曲線
。 在曲線 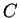 上, 溫度為一
上, 溫度為一  之函數, 如
之函數, 如
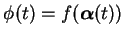 。若
。若 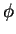 在
在 ![$[a, b]$](img162.gif) 之某一內點
之某一內點 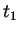 有一極值, 則
有一極值, 則 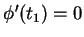 。
另一方面,
連鎖規則又給出
。
另一方面,
連鎖規則又給出
此內積在 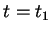 為 0, 因此
為 0, 因此
 垂直
垂直
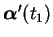 。 但
。 但
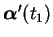 與
與  相切, 故
相切, 故
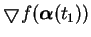 落在垂直
落在垂直 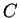 之平面上。
之平面上。
現二梯度向量
 及
及
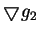 為獨立, 若且唯若其外積
為獨立, 若且唯若其外積
因此
 與
與
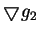 獨立並非表所有上式左側向量之三
Jacobian 皆為 0。 之前我們便已指出, Lagrange
方法只有此條件成立才適用。
獨立並非表所有上式左側向量之三
Jacobian 皆為 0。 之前我們便已指出, Lagrange
方法只有此條件成立才適用。
若
 與
與
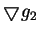 相依, 則此法失效。
例如, 求
相依, 則此法失效。
例如, 求
之極值, 限制條件為
此二曲面之交集為
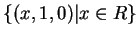 為一直線。 顯然當
為一直線。 顯然當 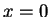 時, 可使
時, 可使 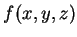 最小, 即極小值發生在
最小, 即極小值發生在 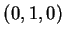 。
但在此點
。
但在此點
且
並無法找到常數 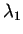 及
及  , 使得
, 使得
例 8.設一救生圈由三部分組成, 中間部分為一圓柱,
前後為二相同的正圓錐, 圓錐的高與圓柱的高等長。 對一給定的表面積,
求此救生圈有最大體積之尺寸。

a
進一步閱讀資料:黃文璋(2002).
極值。微積分講義第九章,國立高雄大學應用數學系。


