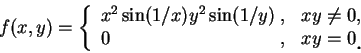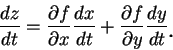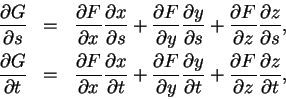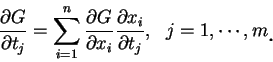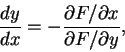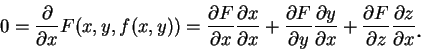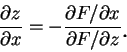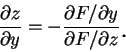合 成 函 數 及 隱 函 數 之 微 分

　　

定理 1.設 $f$ 為一二變數之可微函數, 定義在一 $S\subset R^2$。又設 $P\in S$, $\mbox{\boldmath {$v$}}$ 為一二維向量, 使得 $\{P+t\mbox{\boldmath {$v$}}\vert t\in [0, 1]\}\subset S$。則存在一 $s\in (0, 1)$, 使得

\begin{displaymath} f(P+\mbox{\boldmath {$v$}})-f(P)=D_{\mbox{\small\boldmath {$... ...(P+s\mbox{\boldmath {$v$}})\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(5.1)證明

  a

　　有些二變數函數 $f$, 其混合的二階偏導數$D_{12}f$ 與 $D_{21}f$ 不一定相等。但有時二者會相等。例如, 設

\begin{displaymath} f(x, y)=\sin (xy^2)\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

則

\begin{displaymath} D_1 f(x, y)=y^2\cos (xy^2),\ \ D_2 f(x, y)=2xy\cos (xy^2), \end{displaymath}

因此

\begin{displaymath} D_{12} f(x, y)=D_{21} f(x, y)=2y\cos (xy^2)-2xy^3\sin (xy^2)\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

定理 2.設有一函數 $f(x, y)$, $S$ 為 $R^2$ 中之一開集合。若在 $S$ 中, $D_{12}f$ 及 $D_{21}f$ 皆存在且連續, 則                                                                                   

\begin{displaymath} D_{12} f(P)=D_{21} f(P),\ \forall P\in S\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(5.2)

  a

　　但定理 2 之逆並不成立, 即有可能 (5.2) 成立, 而 $D_{12}f$ 及 $D_{21}f$ 在$P$點並非皆連續。見下例。

例 1.設

\begin{displaymath} f(x, y)=\left\{\begin{array}{lll} x^2\sin(1/x)y^2\sin (1/y) ... ..., & xy=0\mbox{\raisebox{-1.2mm}{\large . }} \end{array}\right. \end{displaymath}

試求$D_{12}f$及 $D_{21}f$ 在(0,0)之值,且$\lim_{(x, y)\to (0, 0)} D_{12}f(x, y)$是否存在？ 

　　　一多變函數 $f$ 若為連續, 且其第一階偏導數亦連續, 則 $f$ 稱為平滑函數。一般而言, 若 $f$ 及其所有至第 $n$ 階之偏導數皆連續, 便稱 $f$ 為 $n$-平滑函數。

　　在第二章對單變函數, 我們以連鎖規則來求合成函數之微分。對多變函數亦有對應的結果。

　

定理 3.設 $F$ 為一定義在開集合 $S$ 之二變數的平滑函數, $f$ 及 $g$ 為二定義在區間 $I$ 之單變函數, 使得 $P(t)=(f(t), g(t))\in S$, $\forall t\in I$。令          

\begin{displaymath} G(t)=F(P(t)),\ t\in I, \end{displaymath}

則

\begin{displaymath} G'(t)=F_1(P(t))f'(t)+F_2(P(t))g'(t)\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(5.3)證明

 　　

　　定理 3 也可改寫為下述形式: 在適當的條件下, 若 $z=f(x, y)$, 其中 $x=x(t)$, $y=y(t)$, 則

\begin{displaymath} \frac {dz}{dt}=\frac {\partial f}{\partial x}\frac {dx}{dt}+... ...}{\partial y}\frac {dy}{dt}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(5.7)

　　另外, 定理 3 中之 $G$ 為一單變函數, 對多變的合成函數, 我們也可有連鎖規則。例如, 設有一函數 $F(x, y, z)$, 且 $x=x(s, t)$, $y=y(s, t)$, $z=z(s, t)$, 又令

\begin{displaymath} G(s, t)=F(x(s, t), y(s, t), z(s, t)), \end{displaymath}

則

\begin{eqnarray*} \frac {\partial G}{\partial s} &=& \frac {\partial F}{\partial... ...t}+\frac {\partial F}{\partial z}\frac {\partial z}{\partial t}, \end{eqnarray*}

只要上述這些導數在一適當的集合中存在且連續。上二式之證明除了包含三個變數外, 其餘部分與定理 3 完全相同。

　　更一般地, 若有一 $n$ 變函數 $F(x_1, x_2,\cdots,x_n)$, 且

\begin{displaymath} x_i=x_i(t_1,\cdots, t_m),\ \ i=1,\cdots,n, \end{displaymath}

又令 $G(t_1,\cdots, t_m)=F(x_1(t_1,\cdots,t_m),\cdots,x_n(t_1,\cdots,t_m))$, 則

\begin{displaymath} \frac {\partial G}{\partial t_j}=\sum_{i=1}^n \frac {\partia... ...tial t_j},\ \ j =1,\cdots,m\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(5.8)

當然所有一階偏導數仍要假設存在且連續。


例 2.設 $F(x, y)=xy^2+x^3+y$, $x=f(t)=t^2-1$, $y=g(t)=2t-t^3$, 又令 $G(t)=F(f(t), g(t))$, 求$G$之一階偏導數。


例 3.設 $z=f(x, y)=x^2+y^2$, $x=g(t)=\cos t$, $y=h(t)=\sin t$。 求。  


例 4.設 $z=x^2+y^2$, $x=r\cos\theta $, $y=r\sin\theta $。分別求 和。  


例 5.設有一函數 $f(x, y)$, $x=r\cos\theta $, $y=r\sin\theta $。令

\begin{displaymath} \phi (r, \theta )=f(r\cos \theta , r\sin\theta )\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

求 ,及。　　

　

 　　其次我們來看隱函數之微分。

　　設 $F(x, y)$ 為一二變數之平滑函數, 且 $f$ 為一可微函數, 使得對每一屬於 $f$ 之定義域 中的 $x$,

\begin{displaymath} F(x, f(x))=0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

利用連鎖規則得

\begin{displaymath} 0=\frac {dF}{dx}=\frac {\partial F}{\partial x}\frac {dx}{dx... ...{\partial y}\frac {dy}{dx}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

由上式可求出 $dy/dx$ 為

\begin{displaymath} \frac {dy}{dx}=-\frac {\partial F/\partial x}{\partial F/\partial y}, \end{displaymath}

上式對每一在 $f$ 之定義域中的 $x$ 且 $F_2(x, f(x))\neq 0$ 成立。


例 6.設 $F(x, y)=x^3+y^3-6xy=0$, 求 $dy/dx$。 

　　設

\begin{displaymath} F(x, y, z)=0, \end{displaymath}

由上式可定義出一函數

\begin{displaymath} z=f(x, y)\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

設 $F$ 與 $f$ 皆為平滑函數。因 $F(x, y, f(x, y))=0$, 由 (5.8) 式得

\begin{displaymath} 0=\frac {\partial }{\partial x}F(x, y, f(x, y))=\frac {\part... ...ac {\partial z}{\partial x}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

又 ${\partial x}/{\partial x}=1$, ${\partial y}/{\partial x}=0$, 因 $x$, $y$ 視為二獨立的變數。因此

\begin{displaymath} \frac {\partial z}{\partial x}=-\frac {\partial F/\partial x}{\partial F/\partial z}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

同理可得

\begin{displaymath} \frac {\partial z}{\partial y}=-\frac {\partial F/\partial y}{\partial F/\partial z}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

　


例 7.設自 $xy^2+yz^2+z^3+x^3-4=0$, 定義出 $z$ 為一 $x$, $y$ 之函數. 求 ${\partial z}/{\partial x}$ 及 ${\partial z}/{\partial y}$。  


例 8.由二方程式

\begin{displaymath} 2x=v^2-u^2,\ \ y=uv, \end{displaymath}

可定義出 $u$, $v$ 為 $x$ 及 $y$ 之函數。求 $\partial u/\partial x$, $\partial u/\partial y$, $\partial v/\partial x$, $\partial v/\partial y$。 

  a

進一步閱讀資料：黃文璋(2002). 合成函數及隱函數之微分。微積分講義第九章，國立高雄大學應用數學系。