|
  
方 向 導 數
a
我們先考慮兩個變數的情況。設  為一二變數函數, 為一二變數函數, 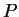 為一在 為一在  之定義 域
之定義 域 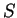 中的點, 中的點, 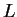 為 為 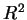 上一條通過 上一條通過 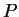 之直線。若將 之直線。若將
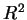 視為 視為 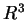 中之 中之 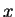 - -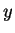 平面, 則通過 平面, 則通過 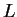 且垂直 且垂直 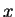 - -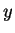 平面之平面
平面之平面 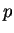 , 交 , 交  之圖形於 一曲線 之圖形於 一曲線 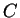 , ,  稱為 稱為  之圖形在平面
之圖形在平面 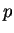 的一截域 。 在 的一截域 。 在 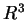 中, 集合 中, 集合
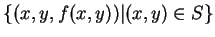 即為 即為  之圖形。由幾何上的性質知, 之圖形。由幾何上的性質知,  可表示為 可表示為
其中
 為一二維之非零向量。 為一二維之非零向量。 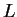 即為一經過 即為一經過 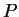 點且方向為 點且方向為
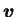 之直線。又對一向量 之直線。又對一向量 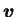 , 我們以 , 我們以
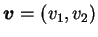 表其二分量分別為
表其二分量分別為 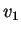 及 及 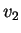 。 。 若將
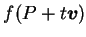 視為一 視為一 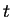 之函數, 則此函數在 之函數, 則此函數在 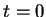 之導數以 之導數以
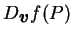 表之。即 表之。即
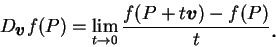 |
(3.1) |
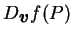 便稱為 便稱為  在 在 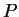 點且方向為 點且方向為
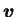 之導數。若令 之導數。若令
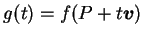 , 則 (3.1) 之右側即為 , 則 (3.1) 之右側即為  , 故 , 故
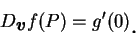 |
(3.2) |
又若將 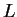 取為一座標軸, 取為一座標軸, 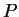 取為原點, 另一軸取為與 取為原點, 另一軸取為與 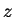 軸平行,
則 軸平行,
則 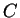 即為 在平面 即為 在平面 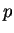 上 上 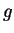 之圖形。 之圖形。
例 1.令
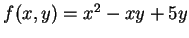 。 求 。 求  在 在 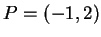 且方向
且方向
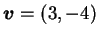 之導數。 之導數。 
仍令
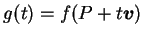 , 且令 , 且令
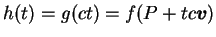 , , 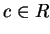 ,
則由連鎖規則得 ,
則由連鎖規則得 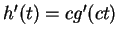 。令 。令 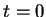 , 即證出 , 即證出
因此
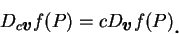 |
(3.3) |
若
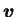 為一單位向量, 即 為一單位向量, 即
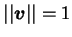 , 則 , 則
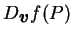 稱為 稱為  在
在 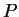 點且方向為 點且方向為
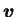 之方向導數。 之方向導數。
若 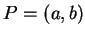 , ,
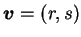 , 且 , 且
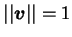 , 即 , 即 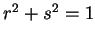 , 則 , 則
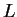 之參數式為 之參數式為
因此前述曲線 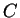 上任一點可以 上任一點可以
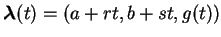 表之。再度由幾何 中的結果知, 曲線
表之。再度由幾何 中的結果知, 曲線 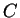 在點 在點
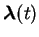 的切向量為
又 的切向量為
又
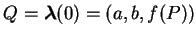 為對應 為對應 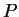 點之 點之  的圖形上的點。故在 的圖形上的點。故在 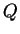 點之切向量為 點之切向量為
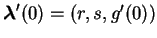 , 此向量即稱為 , 此向量即稱為  之圖形在
之圖形在 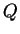 點 且方向為 點 且方向為
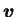 之切向量。此向量之斜率為 之切向量。此向量之斜率為
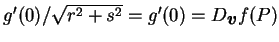 ,
其中最後一等式用到 (3.2) 式。故方向導數即為 ,
其中最後一等式用到 (3.2) 式。故方向導數即為  之圖形上,
在所給定方向之切向量的斜率。
之圖形上,
在所給定方向之切向量的斜率。
例 2.令
 , 求 , 求  在 在 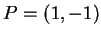 且方向為 且方向為
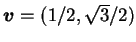 之方向導數。 之方向導數。 
例 3.令
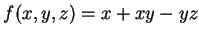 , , 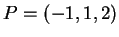 , ,
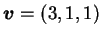 ,
求 ,
求
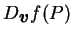 。 。  設有一函數  , 則過 , 則過 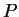 點, 只要給一方向 點, 只要給一方向
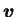 ,
便可有一方向導數。其中在 ,
便可有一方向導數。其中在
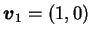 及 及
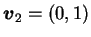 之方向導數特別重要。若
之方向導數特別重要。若 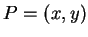 , 則 , 則
可看出
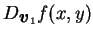 即為固定 即為固定 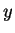 , 將 , 將  視為一 視為一 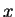 之函數的導數, 而
之函數的導數, 而
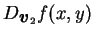 則為固定 則為固定 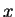 , 將 , 將
 視為一 視為一 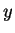 之函數的導數。通常我們以 之函數的導數。通常我們以 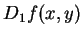 表 表
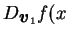 , ,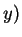 , 以 , 以 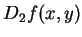 表 表
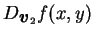 . .
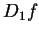 及 及 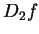 仍為 仍為 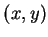 之函數, 並稱為 之函數, 並稱為  之一階偏 導數 。 之一階偏 導數 。
當變數為 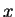 , , 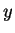 時, 時,
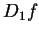 及 及 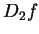 分別稱為 分別稱為  對 對 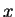 及 及 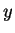 之一階偏導數。對偏導數尚有一些常用的記號:
符號 之一階偏導數。對偏導數尚有一些常用的記號:
符號 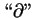 仍發音 “ 仍發音 “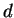 ”, 只是在多變函數裡,
為了與單變函數之導數符號區別, 我們以 ”, 只是在多變函數裡,
為了與單變函數之導數符號區別, 我們以
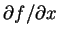 取代 取代
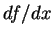 。 。
例 4.令
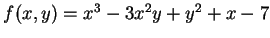 , 求 , 求  之一階偏導數。 之一階偏導數。  例
5.令
 , 求 , 求  之一階
偏導數。 之一階
偏導數。 
當  為一二變數函數, 為一二變數函數, 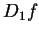 及 及 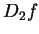 皆仍為二變數函數,
因此我們可再討論 皆仍為二變數函數,
因此我們可再討論 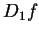 及 及 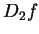 之一階偏導數, 即 之一階偏導數, 即 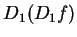 , ,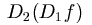 ,
, 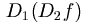 及 及 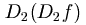 。此四函數稱為 。此四函數稱為  之二階偏導數。 對二階偏導數,
常用的記號為
之二階偏導數。 對二階偏導數,
常用的記號為
注意, 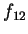 與 與 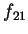 之定義並不相同, 前者為先對 之定義並不相同, 前者為先對 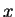 微分再對
微分再對 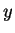 微分, 後者為先對 微分, 後者為先對 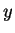 微分再對 微分再對 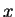 微分。微分為一關於極限的運算, 而我們已提過多次, 兩個有關極限的運算,
若交換其運算次序, 結果並不一定相同。 微分。微分為一關於極限的運算, 而我們已提過多次, 兩個有關極限的運算,
若交換其運算次序, 結果並不一定相同。 同理, 若  為一三變數函數, 則 為一三變數函數, 則  有 9 個二階偏導數,
當然這些二階偏導數當中, 有些可能會相等。有了二階偏導數,
當然可再定義三階偏導數等高階偏導數。例如, 設有一函數 有 9 個二階偏導數,
當然這些二階偏導數當中, 有些可能會相等。有了二階偏導數,
當然可再定義三階偏導數等高階偏導數。例如, 設有一函數 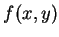 ,
則 ,
則
其中 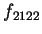 也可寫成 也可寫成
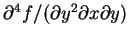 ,
但卻不一定等於 ,
但卻不一定等於
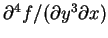 。 。
例 6.令
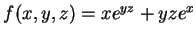 , 求 , 求 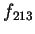 及 及
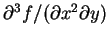 。 。 
例 7.令
求 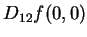 及 及 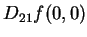 。 。 
a
進一步閱讀資料:黃文璋(2002).
方向導數。微積分講義第九章,國立高雄大學應用數學系。
  
|