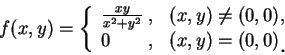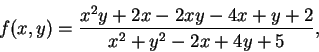|
  
極
限 及 連 續
a
單變數裡極限的概念可以很容易地推廣至多變函數。設
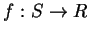 , 其中 , 其中 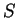 為 為 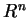 之一子集, 即 之一子集, 即 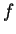 為一以 為一以 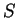 為定義域 之
為定義域 之 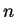 個變數的函數。則對 個變數的函數。則對
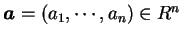 , 可以 , 可以
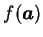 表 表
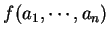 . 對一 . 對一 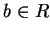 , ,
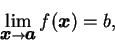 |
(2.1) |
或寫成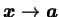 時, 時, 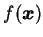 →
→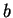 , 表 , 表
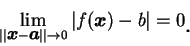 |
(2.2) |
(2.2) 式又等價於
 |
(2.3) |
(2.1) 式也可以鄰域來說明。即 (2.1)
式成立, 若且唯若對每一 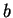 之鄰域
之鄰域 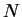 , 存在一 , 存在一
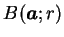 , 使得只要 , 使得只要
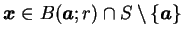 , 則 , 則
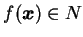 。若 。若
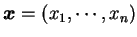 , ,
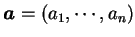 , 則 , 則
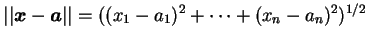 。 。
故
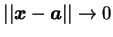 , 若且唯若 , 若且唯若 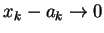 , ,
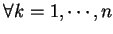 。 。
對 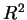 中的點, 若以 中的點, 若以 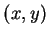 表 表
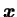 , , 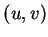 表 表
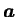 , 則 (2.1) 式可寫成 , 則 (2.1) 式可寫成
至於對 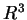 中的點, 若以 中的點, 若以 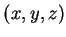 表 表
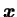 , , 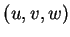 表 表
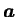 , 則 (2.1) 式可寫成 , 則 (2.1) 式可寫成
一函數 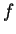 , 若滿足 , 若滿足
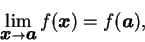 |
(2.4) |
則稱在
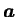 連續。 若 連續。 若 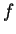 在 在
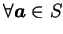 連續, 則稱 連續, 則稱 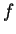 在 在
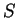 連續。 連續。
例 1.設 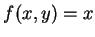 , ,  , 試證 , 試證 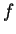 為一連續函數。 為一連續函數。 
由於上述多變函數之極限及連續的定義,
本質上與單變函數裡的定義是一樣的, 因此可以預期的,
許多以前有的關於極限及連續的結果,
在多維裡也有對應的結果。
a
定理 2.設 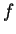 及 及 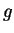 為二 為二 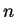 變數函數且皆在 變數函數且皆在
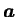 點連續。則 點連續。則 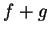 , ,
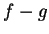 及 及 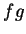 皆在 皆在
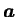 點連續, 且只要 點連續, 且只要
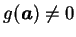 , 則 , 則 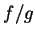 在
在
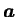 點亦連續。 點亦連續。
|
a
一函數若為一些
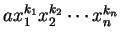 之和, 其中 之和, 其中 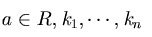 為非負整數, 便稱為一 為非負整數, 便稱為一 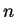 變數之多項函數。 例如,
變數之多項函數。 例如,
為一二變數之多項式。二多項式之商則為一有理函數。不難看出每一 多項式皆為連續函數,
每一有理式在分母不為 0 處亦連續。經由合成函數之連續性定理, 可得許多函數為連續。因此諸如
, 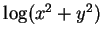 , ,
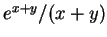 及
, 在其有定義處皆連續。
故第一個函數在整個 - 及
, 在其有定義處皆連續。
故第一個函數在整個 -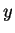 平面皆連續, 第二個函數在 平面皆連續, 第二個函數在
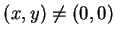 處連續, 第三個函數在 處連續, 第三個函數在 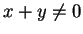 處連續, 第四個函數在 處連續, 第四個函數在
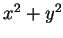 不為 不為 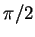 之奇數倍處連續。上述這幾個例子顯示,
對一二變數函數, 其不連續點的集合, 可能包含一些隔離的點, 一條曲線或一些曲線。
底下我們給一二變數函數,
對每一變數皆連續, 但若視為一二變數的函數,
則不為連續。 之奇數倍處連續。上述這幾個例子顯示,
對一二變數函數, 其不連續點的集合, 可能包含一些隔離的點, 一條曲線或一些曲線。
底下我們給一二變數函數,
對每一變數皆連續, 但若視為一二變數的函數,
則不為連續。
例 2.令
固定 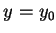 , 若 , 若 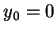 , 則 , 則 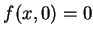 , ,
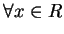 , 故 , 故 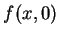 為一連續函數; 若 為一連續函數; 若 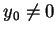 , 則 , 則
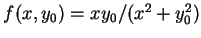 為一分母不為 0 之 有理式, 故仍為連續函數。因此對每一固定的
為一分母不為 0 之 有理式, 故仍為連續函數。因此對每一固定的 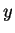 , ,
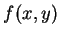 為一 為一 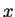 之連續函數。同理, 若固定 之連續函數。同理, 若固定 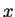 , , 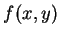 仍為一
仍為一 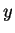 的連續函數。 的連續函數。
但若 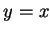 , 且 , 且
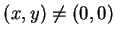 , 則 , 則
故若 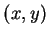 沿著直線 沿著直線 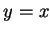 趨近至 趨近至 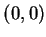 , 則 , 則
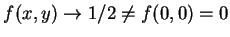 . 因此若視為一二變數的函數,
則 . 因此若視為一二變數的函數,
則 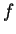 在 在 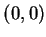 不連續。事實上, 若 不連續。事實上, 若 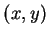 沿著直線 沿著直線 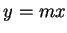 趨近至 趨近至 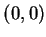 , 則 , 則
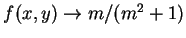 。在本例裡, 雖
且
但 。在本例裡, 雖
且
但
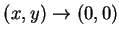 時, 時, 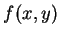 之極限卻不存在。
也就是雖二逐次極限皆存在且相等,
但兩變數函數之極限卻有可能不存在。 之極限卻不存在。
也就是雖二逐次極限皆存在且相等,
但兩變數函數之極限卻有可能不存在。
對一二變數的函數, 其不連續性, 較單變數的函數複雜許多。此因對一單變函數,
“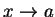 ” 只分為 ” 只分為 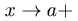 及 及 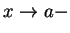 , 即分別從 , 即分別從 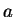 之右側及左側趨近至 之右側及左側趨近至 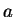 。 但在平面上, 。 但在平面上,
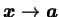 , ,
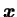 可有各種方式趨近至 可有各種方式趨近至
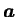 , 如可沿一直線、或一曲線接近 , 如可沿一直線、或一曲線接近
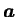 。 此時要檢驗連續性當然比較麻煩,
但只要發現 。 此時要檢驗連續性當然比較麻煩,
但只要發現
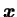 沿著某一曲線趨近至
沿著某一曲線趨近至
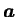 時, 時,
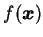 並不趨近至 並不趨近至
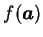 , 便可判定 , 便可判定
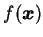 在 在
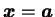 不連續。 不連續。
例 3.令 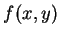
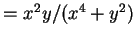 , , 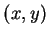  。當 。當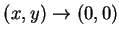 時, 時,
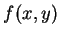 之極限是否存在。 之極限是否存在。 
例 4.令
求
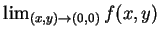 。 。 
例 5.分別討論下述二函數之連續性。
(i)
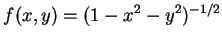 ; ; (ii)
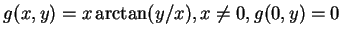 。 。 
例 6.令
求
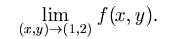 
a
進一步閱讀資料:黃文璋(2002).
極限及連續。微積分講義第九章,國立高雄大學應用數學系。
  
|