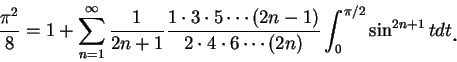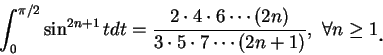|
其 他 關 於 級 數 的 結 果 a 無限級數是將一數或函數以一無限的過程來表示的一種方式, 但並非唯一的方式。無限的乘積是其他的方式之一。例如 Wallis 乘積, 即
表部分乘積數列
之極限, 只要此極限存在。因此
此美妙的公式, 其重要性並不亞於
欲了解 (6.2) 式, 我們先看一下較簡單的多項式。設
當然其中之
其中令 現若
又利用
則由 (6.3) 即得 (6.1) 式。 我們再看與 7.3 節曾定義過的 zeta 函數之一相關問題。令人驚訝的是, 函數
與質數有一重要的關係。對質數
故由幾何級數
對
至於右側, 因每一大於 1 之整數, 有唯一之質因數乘積表示法, 故右側為
因此 zeta 函數可表示成下述乘積
由 (6.4) 式亦可導出質數有無限多個。此因若只有有限多個質數, 以
利用冪級數展式, 除了可以求函數之數值外, 也可藉此擴展一些函數的定義域至複數。 例如, 由
指數函數的定義域本來是實數, 對每一複數
我們只要定義
這就是歐拉公式。由此立即得到
這是一個很有趣且典雅的式子, 它包含差不多是數學中最重要的5個數及二符號。 指數及三角函數, 是自然界最巧妙的兩類函數, 經由冪級數, 可建立起其間的關係。 不過嚴格地講, 以這樣的方法推導出
並不是很嚴密。此因
首先, 各位在中學時代可能已學過 De Moivre 公式 : 對每一整數
若以
對一固定的
故
雖然在 5.3
節我們所得到的
另外, 我們也可以冪級數, 以完全解析的方法來定義諸如 sine 函數及 cosine 函數, 而我們熟悉的三角函數的許多其他的性質皆可以這些展式得到。除了在上一節看過的, 可得到微分公式外, 其他如
都立即可得。加法公式也可如下獲得。令
其中
則易證
故
因此
至於 我們再看一藉由級數之發散來判斷一數列之一般項趨近至 0 的結果。先給一例子。利用 Stirling 公式 , 立即可得若
則
故交錯級數
a 回到定理 1 之前的交錯級數
另外, 利用定理 1 也可極容易地得到諸如
及二項式級數
收斂。 底下為一關於兩冪級數相乘的結果。
這種函數很多, 但並非我們常見的函數, 底下給一例。令
再擴展
則
因
至於 我們提過多次, 多項式是最簡單的函數。對每一閉區間上的連續函數,
可以一數列之多項式 來均勻逼近。
如果一函數有冪級數展式, 則可取其冪級數之部分和來均勻逼近該函數。不過此定理的特殊性在於只要對連續函數
其次我們看 Abel 極限定理。首先若
我們知道上式右側對
下述定理指出答案是肯定的。
定理 5 有下述的推論, 其證明也要用到定理 6.2, 請見 Apostol
(1973) Theorem 9.32。
在 7.3
節我們曾給一歐拉發現有關
此公式有許多不同的證法, 。底下我們提供一只需利用至今所學的工具的基本證法。 首先利用絕對收斂級數的性質, 下式成立:
故若能證出
即得證 (6.17)。
利用 Raabe 檢定法 , 可證明 (6.19) 之右側級數當
將 (6.20) 之左、右分別由 0 至
第三章 (4.13) 式又給出
將 (6.22) 代入 (6.21) 即得 (6.18)。 證畢。
最後我們來看 Tauber 定理 。一般而言, 定理
5
之逆定理並不成立。即若
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
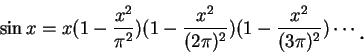
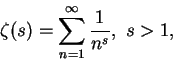
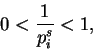

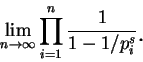
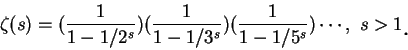
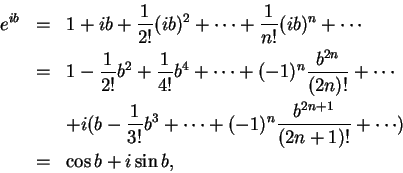
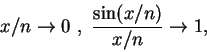
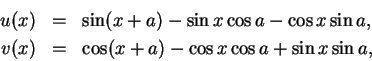
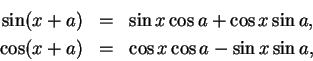
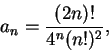
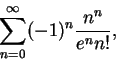
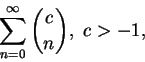
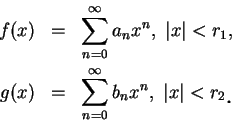
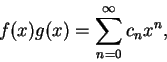
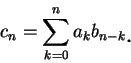
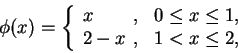
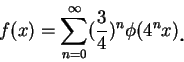

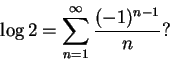
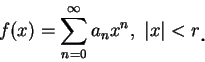

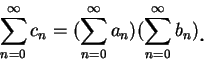
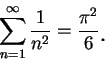
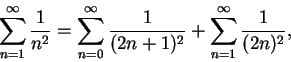

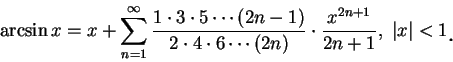
![\begin{displaymath}
\hspace*{1cm} t=\sin t+\sum_{n=1}^{\infty}\frac {1\cdot 3\cd...
...rac {\pi} 2,
\frac {\pi} 2]\mbox{\raisebox{-1.2mm}{\large . }}
\end{displaymath}](img153.gif)