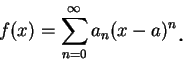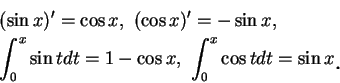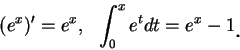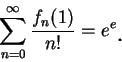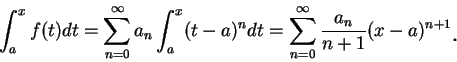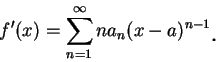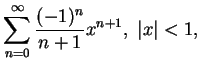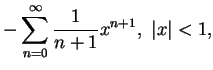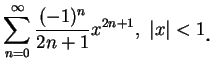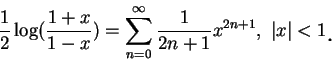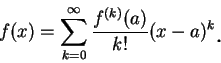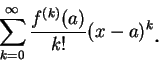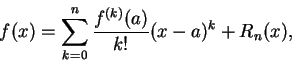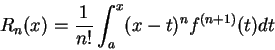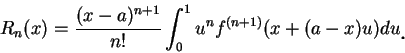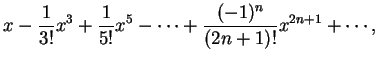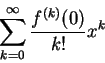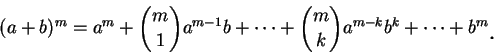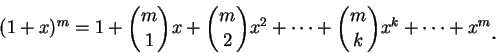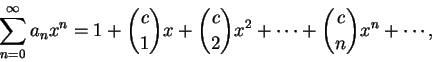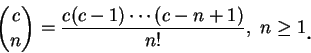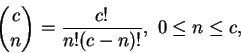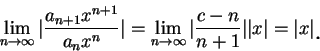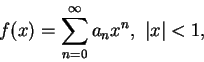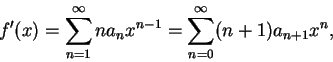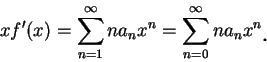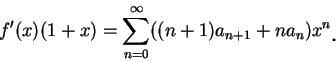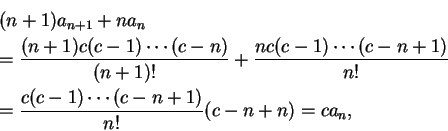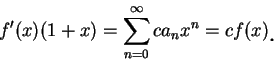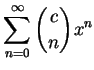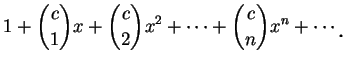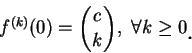|
  
冪
級 數
之 性 質
a
給一冪級數
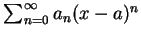 , 對每一屬於其收斂區間的 , 對每一屬於其收斂區間的 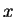 ,
定義函數 ,
定義函數  為 為
我們稱級數
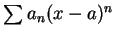 為 為  關於 關於 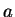 之冪級數展式 , 或稱為 之冪級數展式 , 或稱為  之冪級數表示法。
之冪級數表示法。 對冪級數展式, 我們可能會對下述問題感到興趣:
(i) 給一級數討論其和函數  之性質; 之性質;
(ii) 討論何時一函數有冪級數展式。
a
由 (5.2) 知,  之積分仍有冪級數表示法。再由定理 4.3
知,
此二級數有相同的收斂半徑。 之積分仍有冪級數表示法。再由定理 4.3
知,
此二級數有相同的收斂半徑。
|
定理 2.設  在區間 可表示成 (5.1) 式,
其中 在區間 可表示成 (5.1) 式,
其中 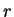 表冪級數之收斂半徑。則 表冪級數之收斂半徑。則
(i) 微分級數
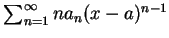 之收斂半徑仍為 之收斂半徑仍為 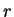 ; ;
(ii) 對
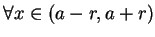 , , 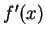 存在, 且 存在, 且
|
a
由於有定理 1 及 2, 在
8.1 節我們經由逐項微分或積分, 而得到新的冪級數
之運算皆是合法的。特別地, 我們有下述展式:
由 (5.3) 及 (5.4) 得
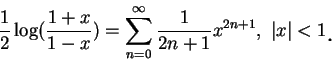 |
(5.6) |
當 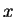 由 由 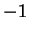 移動至 1 時, 移動至 1 時, 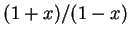 取值在所有正數上。故只要適當地選取 取值在所有正數上。故只要適當地選取 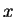 值, 我們可由 (5.6) 式得到任一正數之對數值。 值, 我們可由 (5.6) 式得到任一正數之對數值。
定理 2 之另一推論為一冪級數之和函數之任意階導數皆存在,
且可經由逐項微分而得。若
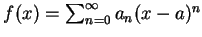 , 則經微分 , 則經微分 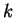 次後且令
次後且令 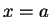 得 得
故 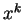 之係數為 之係數為
至於
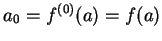 。故 。故  之冪級數展式為 之冪級數展式為
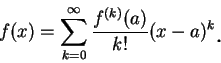 |
(5.7) |
此性質即為冪級數展式之唯一性定理 。
a
由 (5.7) 式亦可看出一冪級數之部分和, 即為其和函數在 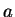 之泰勒展式。換句話說, 若函數
之泰勒展式。換句話說, 若函數  在區間 在區間 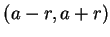 可表示成一冪級數, 則
可表示成一冪級數, 則  在 在 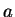 之 泰勒多項式數列, 在 之 泰勒多項式數列, 在 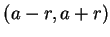 中逐點收斂至和函數 中逐點收斂至和函數  。尤有進者, 在 。尤有進者, 在 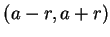 之任一閉的子區間, 此為均勻收斂。接著我們來看本節一開始所提出的第二個問題, 即給定一函數
之任一閉的子區間, 此為均勻收斂。接著我們來看本節一開始所提出的第二個問題, 即給定一函數  ,
何時可在 ,
何時可在  點之某一鄰域有冪級數展式? 點之某一鄰域有冪級數展式? 前面已證過, 這種函數必在  之某一鄰域的每一階導數皆存在 (因此 之某一鄰域的每一階導數皆存在 (因此
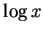 與 與 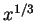 在 0 皆無法展開, 因二者在 在 0 皆無法展開, 因二者在 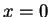 之導數皆不存在), 且此函數之冪級數展式如 (5.7) 所給。現設有一在
之導數皆不存在), 且此函數之冪級數展式如 (5.7) 所給。現設有一在
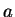 之某一鄰域的任意階導數皆存在的函數 之某一鄰域的任意階導數皆存在的函數  ,
這種函數稱為在該區間無限次可微 。則我們可寫出下述 冪級數 ,
這種函數稱為在該區間無限次可微 。則我們可寫出下述 冪級數
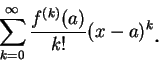 |
(5.8) |
此級數稱為由  在 在 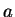 所產生之泰勒級數 。 我們立刻會問: 除了在 所產生之泰勒級數 。 我們立刻會問: 除了在 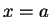 外, 此級數是否會收斂? 如果是的話, 其和是否等於 外, 此級數是否會收斂? 如果是的話, 其和是否等於 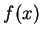 ? 令人訝異的是,
一般而言此二問題的答案皆為否定。除了在 ? 令人訝異的是,
一般而言此二問題的答案皆為否定。除了在 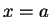 外, 此級數不一定收斂, 即使收斂, 其和也不一定等於 外, 此級數不一定收斂, 即使收斂, 其和也不一定等於 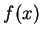 。底下我們給使此二問題之答案皆為肯定之充要條件。 。底下我們給使此二問題之答案皆為肯定之充要條件。
首先由第四章 (3.15)
式之泰勒公式知
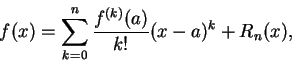 |
(5.9) |
等號右側之有限項的和為  在 在 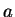 之 之 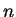 次泰勒多項式, 次泰勒多項式, 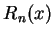 為餘項, 也就是以泰勒多項式來逼近
為餘項, 也就是以泰勒多項式來逼近  之誤差。若在 (5.9) 中令 之誤差。若在 (5.9) 中令
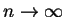 , 則可看出 (5.8)之冪級數會收斂至 , 則可看出 (5.8)之冪級數會收斂至 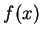 , 若且唯若誤差項 , 若且唯若誤差項
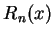 趨近至 0。底下定理 4 及 5 給出使此誤差項趨近至 0
的充分條件。 趨近至 0。底下定理 4 及 5 給出使此誤差項趨近至 0
的充分條件。
在第四章 (3.19) 式我們將 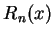 表示成一積分, 即 表示成一積分, 即
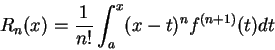 |
(5.10) |
只要 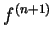 在 在 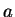 之某一鄰域連續, 且 之某一鄰域連續, 且 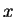 屬於此鄰域,
上式便成立。故若 屬於此鄰域,
上式便成立。故若  無限次可微, 對 無限次可微, 對
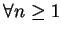 ,
我們皆可將誤差表示成上式, 因此泰勒級數 收斂至 ,
我們皆可將誤差表示成上式, 因此泰勒級數 收斂至 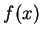 , 若且唯若
(5.10) 之右側, 當 , 若且唯若
(5.10) 之右側, 當
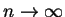 時趨近至 0。 時趨近至 0。
利用變數代換, 令 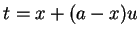 , 則 , 則 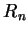 可改寫為 可改寫為
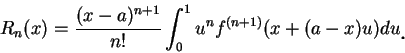 |
(5.11) |
我們有下述定理。
a
例 1.令 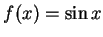 , , 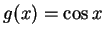 。 因 。 因
故不論對 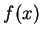 或 或 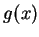 , (5.12) 式成立, 其中 , (5.12) 式成立, 其中 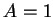 。 因此 。 因此
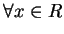 。利用定理 1 及 2, 由上述二展式, 立即可看出 。利用定理 1 及 2, 由上述二展式, 立即可看出
例 2.令 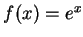 。 首先 。 首先
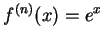 , ,
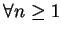 , , 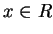 。 又對 。 又對 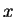 在任一有限區間 在任一有限區間 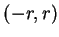 中,
其中 中,
其中 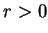 , , 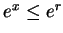 , 而 , 而 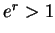 , 因此 (5.12) 式成立, 其中 , 因此 (5.12) 式成立, 其中
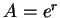 。因 。因 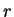 可為任意一正數, 即得證對 可為任意一正數, 即得證對
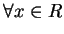 , 下式成立: , 下式成立:
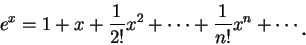 |
(5.15) |
由此展式也可看出
例 3.求下述級數和。
例 4.令 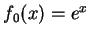 , 且 , 且
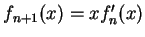 , ,
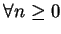 。試證 。試證
定理 4 指出, 若一函數  之 之 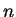 階導數 階導數 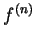 成長的速度小於某正數 之
成長的速度小於某正數 之 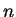 次方, 則 次方, 則  之泰勒級數收斂至 之泰勒級數收斂至  。 。
a
由二項式定理, 對每一正整數 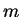 , 我們有 , 我們有
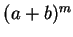 表 表
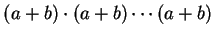 連乘 連乘 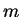 項,
因此上述公式其實是用到 排列組合的技巧。但若 項,
因此上述公式其實是用到 排列組合的技巧。但若 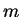 不為正整數呢?
我們先取 不為正整數呢?
我們先取 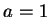 , , 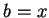 , 並考慮 , 並考慮 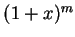 。則若知 。則若知 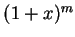 之展式, 一般的
之展式, 一般的
便也能寫出, 只要 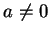 。 。
當 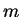 為正整數時, 為正整數時,
若 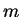 不為正整數, 我們仍可將 不為正整數, 我們仍可將 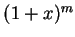 表示成一級數,
只是此時級數便不會終止了。 我們會得到 一所謂的二項式級數,
且其形式為 (以 表示成一級數,
只是此時級數便不會終止了。 我們會得到 一所謂的二項式級數,
且其形式為 (以 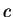 取代 取代 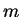 ): ):
|
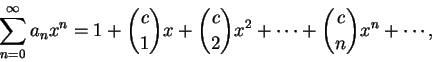
|
(5.20)
|
此處
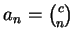 , 而 , 而
|
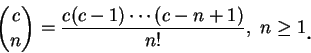
|
(5.21)
|
注意當 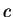 為一非負整數時, 由 (5.21) 得 為一非負整數時, 由 (5.21) 得
|
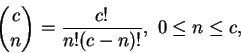
|
(5.22)
|
此與我們過去中學時代在學排列組合中, 所得相同。故 (5.21) 即推廣
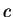 不為非 負整數時 不為非 負整數時 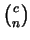 的意義, 而 (5.22)
中之等號右側因有 的意義, 而 (5.22)
中之等號右側因有 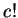 , 故只對 , 故只對 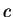 為 非負整數時才成立。又由
(5.21) 可看出, 當 為 非負整數時才成立。又由
(5.21) 可看出, 當 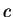 為一非負整數時, 對 為一非負整數時, 對 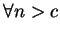 , ,
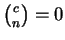 , 此時 (5.20) 成為一有限的級數。除此情況外, (5.20) 皆為一無限級數。 , 此時 (5.20) 成為一有限的級數。除此情況外, (5.20) 皆為一無限級數。 我們再來看 (5.20)
之級數的收斂半徑。由比值檢定法, 因
故當 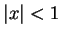 , 級數收斂; 當 , 級數收斂; 當 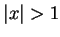 , 級數發散, 即收斂半徑為 1。 , 級數發散, 即收斂半徑為 1。
對
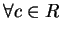 , (5.20) 之二項式級數, 定義一函數 , (5.20) 之二項式級數, 定義一函數  如下: 如下:
|
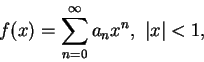
|
(5.23)
|
若 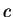 為一非負整數, 由二項式定理, 為一非負整數, 由二項式定理,  即成為 即成為
|
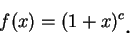
|
(5.24)
|
底下證明, 事實上對
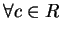 , ,  皆有上述形式。 皆有上述形式。
而若能證出
|

|
(5.25)
|
則
其中 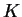 為一常數。又因 為一常數。又因 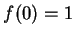 , 故 , 故 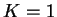 。 如此一來 (5.24)
對 。 如此一來 (5.24)
對
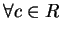 便成立了。 便成立了。 我們便開始證明 (5.25)。即要證明
將上式每一項各乘以 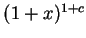 得 得
|
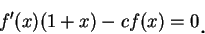
|
(5.26)
|
底下證明 (5.23) 定義出之  滿足 (5.26)。 滿足 (5.26)。
由定理 5.2, 對 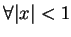 , ,
故
因此
又
故
如此即證出 (5.26) 成立, 因此 (5.25) 成立, 故 (5.24) 成立。證畢。
我們將結果陳述於下, 此即推廣的二項式定理。
|
定理 6.對
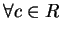 , , 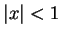 , ,
|
a
我們展開 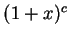 而非 而非
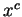 , 此因後者在 , 此因後者在 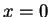 並非所有導數皆存在, 除非 並非所有導數皆存在, 除非 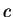 為一
非負整數, 而此時 為一
非負整數, 而此時 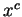 已為一冪級數了。另外,
我們是以間接的手法證出 已為一冪級數了。另外,
我們是以間接的手法證出 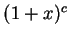 之展式如 (5.27), 亦可直接導出。即令 之展式如 (5.27), 亦可直接導出。即令  , 則極易看出 , 則極易看出
故若能證出
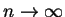 時, 餘項 時, 餘項 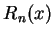 趨近至 0, 則由定理 5 便得到
(5.27) 成立了。 趨近至 0, 則由定理 5 便得到
(5.27) 成立了。
例 5.求 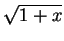 之展式。 之展式。 
例 6.求
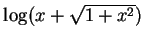 之展式。 之展式。 
a
進一步閱讀資料:黃文璋(2002).
冪級數之性質。微積分講義第八章,國立高雄大學應用數學系。
  
|