|
  
冪
級 數
a
若一無限級數有下述形式
便稱為一 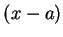 之冪級數。 之冪級數。
a
對一 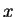 (即 (即 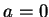 的情況) 之冪級數, 其收斂範圍為一以 0
為中心的區間。 的情況) 之冪級數, 其收斂範圍為一以 0
為中心的區間。
a
定理 2 指出, 對一冪級數 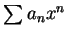 , 使其收斂的範圍, 必是一連續的以 0
為中心之區間 (也可能只有 0 這一點)。至於若有一 , 使其收斂的範圍, 必是一連續的以 0
為中心之區間 (也可能只有 0 這一點)。至於若有一 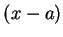 之冪級數, 也立即可寫出對應的定理 1 及 2,
此時收斂區間是以 之冪級數, 也立即可寫出對應的定理 1 及 2,
此時收斂區間是以 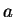 為中心。
不過定理 2 並未能告訴我們級數 為中心。
不過定理 2 並未能告訴我們級數 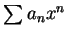 在 在 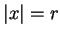 是否收斂。 對
是否收斂。 對 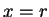 或 或 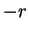 , 要單獨判斷級數之斂散性。
由於有定理 2, 我們稱 , 要單獨判斷級數之斂散性。
由於有定理 2, 我們稱 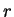 為 為 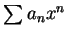 之收斂半徑 。可看出收斂半徑亦可定義為使 之收斂半徑 。可看出收斂半徑亦可定義為使 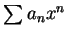 收斂之所有 收斂之所有 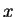 的集合之最小上界。冪級數在其收斂區間的內點收斂,
但在該區間的端點就不一定收斂了。又
的集合之最小上界。冪級數在其收斂區間的內點收斂,
但在該區間的端點就不一定收斂了。又 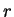 也可能為 0, 即 也可能為 0, 即 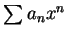 只有當 只有當 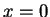 才收斂, 此時級數和為 才收斂, 此時級數和為 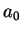 ; ; 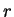 也可能為 也可能為
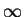 , 此時對 , 此時對
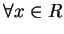 , 皆使級數收斂, 因此收斂區間為 , 皆使級數收斂, 因此收斂區間為
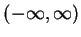 。 另外, 由定理 1
知, 。 另外, 由定理 1
知, 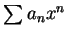 在每一區間 在每一區間 ![$[-b, b]$](img56.gif) 均勻收斂, 其中
均勻收斂, 其中 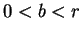 。 。
例 1.求下述各級數之收斂半徑 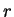 及收斂區間。 及收斂區間。 
(i) 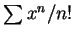 ; ;
(ii)
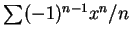 ; ;
(iii) 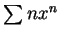 ; ; (iv)
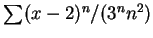 。 。
一冪級數的係數若做一些改變有時並不影響其收斂半徑。
一個特例是若將 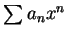 之每一項皆除以 之每一項皆除以 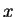 而得 而得
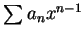 , 或皆乘以 , 或皆乘以 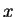 而得到 而得到
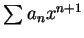 , 皆與原級數有相同之收斂區間。 , 皆與原級數有相同之收斂區間。
|
定理 3.設
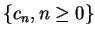 為一數列之正數, 且滿足 為一數列之正數, 且滿足
|
![\begin{displaymath}
\lim_{n\rightarrow \infty }\sqrt [n]{c_n}=1,
\end{displaymath}](img89.gif)
|
(4.2)
|
則 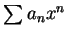 與 與
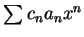 有相同之收斂半徑。 有相同之收斂半徑。
|
a
例 2.因
故感覺上差異很大的三級數
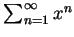 , ,
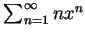 與 與
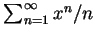 , 有相同的收斂半徑,
且皆為 1。但收斂區間依序為 , 有相同的收斂半徑,
且皆為 1。但收斂區間依序為 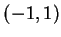 , , 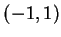 , [-1,1)並不盡相同。 , [-1,1)並不盡相同。
最後, 我們也可考慮較一般的冪級數
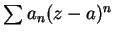 , 其中 , 其中 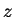 , ,
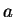 , , 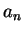 皆為 複數。則本節的結果仍成立,
只是收斂區間要改為收斂圓 。即若收斂半徑 皆為 複數。則本節的結果仍成立,
只是收斂區間要改為收斂圓 。即若收斂半徑
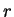 , 則級數在以 , 則級數在以 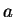 為圓心 為圓心 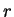 為半徑的圓內收斂, 在圓外發散。至於在 為半徑的圓內收斂, 在圓外發散。至於在 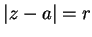 仍要另外討論, 視情況不同會有不同的結論。 仍要另外討論, 視情況不同會有不同的結論。
a
進一步閱讀資料:黃文璋(2002).
冪級數。微積分講義第八章,國立高雄大學應用數學系。
  
|