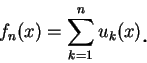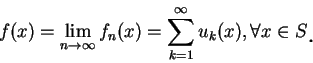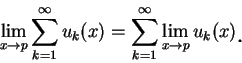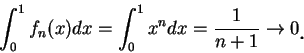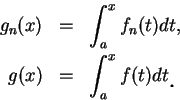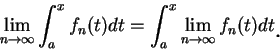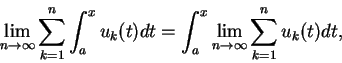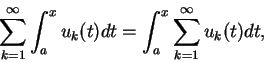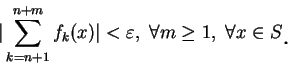|
  
均 勻 收 斂
a
設 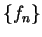 為一在集合 為一在集合  上逐點收斂至 上逐點收斂至  的函數數列。由極限的定義知, 此即表對 的函數數列。由極限的定義知, 此即表對
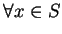 及對 及對
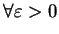 ,
存在一 ,
存在一 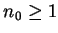 , 使得 , 使得
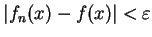 , ,
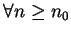 。但上述 。但上述 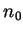 通常會與 通常會與  及 及 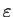 有關。也就是對不同的 有關。也就是對不同的
 或 或 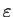 , 所找到的 , 所找到的 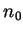 可能不同。但若對 可能不同。但若對
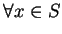 ,
可找到一相同的 ,
可找到一相同的 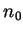 , 則這種收斂便稱為在 , 則這種收斂便稱為在  上均勻收斂 。 上均勻收斂 。
a
均勻收斂可以有一簡單的幾何解釋。首先
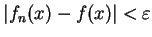 與 與
等價。若上式對
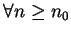 及 及 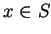 成立, 則所有 成立, 則所有
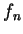 在 在  中的圖形, 便介於一寬度為 中的圖形, 便介於一寬度為 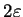 , 以 , 以  為中心軸的帶子中, 見圖3.1. 讀者也可想想為什麼
若不為均勻收斂,
則
為中心軸的帶子中, 見圖3.1. 讀者也可想想為什麼
若不為均勻收斂,
則 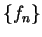 與 與  便沒有如圖 3.1 的關係。 便沒有如圖 3.1 的關係。

圖3.1. 均勻收斂之幾何意義
例 1.令
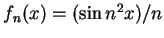 , , 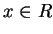 , , 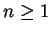 。
取 。
取 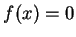 , ,
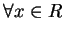 。是否為均勻收斂? 。是否為均勻收斂? 
a
上述定理也可應用至函數級數。對
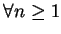 , 設函數 , 設函數 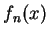 為一函數級數
為一函數級數
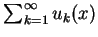 之部分和, 即 之部分和, 即
若在  上 上
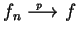 , 則 , 則
此時稱級數 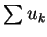 逐點收斂至和函數 逐點收斂至和函數  。若在 。若在  上 上
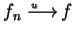 , 則稱級數 , 則稱級數 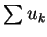 均勻收斂至 均勻收斂至  。 。
a
系理 1 之結果可以下述符號來表示:
此表對一均勻收斂的級數, 我們可交換極限與和二運算。 又附帶一提,
均勻收斂只是傳遞連續性之一充分條件, 並非必要條件。
例 2. 令
則顯然 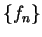 在 在 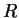 上均勻收斂至 上均勻收斂至 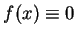 。但雖每一 。但雖每一
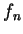 為一到處 不連續之函數, 而極限函數 為一到處 不連續之函數, 而極限函數  卻為一到處連續的函數。
卻為一到處連續的函數。
a
例 3.設 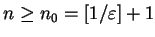 , ,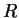 , ,![$x\in [0,1]$](img32.gif) 。由於此為一連續函數數列卻有一不連續的極限函數, 故由定理
1 知, 非在 。由於此為一連續函數數列卻有一不連續的極限函數, 故由定理
1 知, 非在 ![$[0, 1]$](img64.gif) 均勻收斂。但 均勻收斂。但
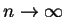 時, 時,
故
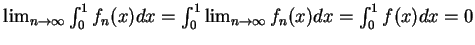 。 。
a
Weierstrass 提供一有用的判別法
,
此法對所給定的函數級數,
若存在一支配它的收斂正項級數便適用。
a
一級數之逐項微分的和是否會等於和之微分呢?
一般而言二者並不相等, 即使是 均勻收斂的情況。例如, 因
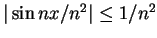 , 故 , 故
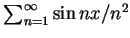 收斂。再由定理
3 知此為均勻收斂。 但此級數逐項微分的和為 收斂。再由定理
3 知此為均勻收斂。 但此級數逐項微分的和為
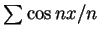 , 在 , 在
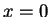 發散。此例顯示即使是均勻收斂,
逐項微分也可能會破壞收斂性。故一般而言, 驗證和及微分之可交換,
比驗證和及積分之可交換難得多。 發散。此例顯示即使是均勻收斂,
逐項微分也可能會破壞收斂性。故一般而言, 驗證和及微分之可交換,
比驗證和及積分之可交換難得多。 在結束本節前,
我們分別給數列及級數之均勻收斂的柯西條件 。
a
a
- 例 4.
- 討論下述各函數數列
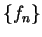 之均勻收歛性。 之均勻收歛性。
(i)
![$f_n(x)=x^n-x^{2n}, x\in [0, 1]$](img107.gif) ; ; |
(ii)
![$f_n(x)=\sin(x/n), \in [-a, a], a>0$](img108.gif) ; ; |
(iii)
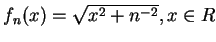 ; ; |
(iv)
![$f_n(x)=nx/(1+nx), x\in [0,1]$](img110.gif) ; ; |
(v)
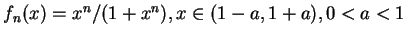 . . |
a
進一步閱讀資料:黃文璋(2002).
均勻收斂。微積分講義第八章,國立高雄大學應用數學系。
  
|