|
  
逐 點 收 斂
a
設有一數列之函數 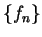 , 且設這些函數有相同的定義域。對每一定義域中的 , 且設這些函數有相同的定義域。對每一定義域中的 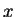 , 可得一數列 , 可得一數列 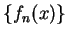 。令 。令 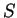 表使此數列收斂的
表使此數列收斂的 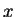 之集合。則一定義在 之集合。則一定義在 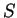 上的函數 上的函數 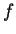 ,其中 ,其中
 |
(2.1) |
稱為數列 {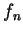 } 之極限函數。並稱數列
{ } 之極限函數。並稱數列
{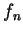 }在 }在 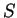 上逐點收斂至 上逐點收斂至 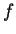 。並以 。並以
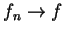 (逐點收斂), 或 (逐點收斂), 或
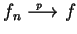 表之。 表之。 由柯西收斂檢定法知, 即使不知極限函數 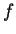 , 我們仍可判定函數數列
{ , 我們仍可判定函數數列
{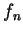 } 是否收斂。也就是 { } 是否收斂。也就是 {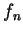 } 收斂至一極限函數,
若且唯若存在一集合 } 收斂至一極限函數,
若且唯若存在一集合 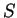 , 且對 , 且對
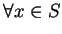 及任一 及任一
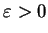 ,
存在一 ,
存在一 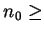 1, 使得對 1, 使得對 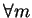 , ,  , ,
對函數數列,
我們主要想討論下述問題: 若數列
{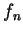 } 中之每一 } 中之每一 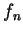 皆有某一性質, 如連續、可微或可積, 則極限函數 皆有某一性質, 如連續、可微或可積, 則極限函數 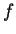 是否亦具有此特性? 底下我們先給幾個例子。 是否亦具有此特性? 底下我們先給幾個例子。例
1.對
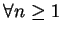 , 令 , 令 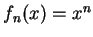 , , ![$x\in [0,1]$](img32.gif) , 則每一 , 則每一 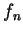 皆為連續函數。 則極限函數 皆為連續函數。 則極限函數 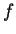 是否亦為連續函數? 是否亦為連續函數?  
例 2.試給一
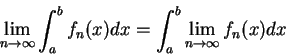 |
(2.3) |
不一定成立之例。 
例 3.試給一可微函數數列 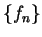 , 極限函數存在, 但 , 極限函數存在, 但 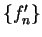 發散之例。
發散之例。 
例 4.設有一二重數列 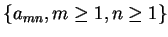 , 其中 , 其中
則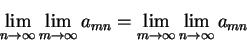 是否成立? 是否成立?  
例 5.對
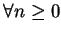 ,令 ,令
則每一 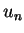 皆為連續函數。令
因 皆為連續函數。令
因 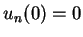 , ,
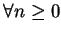 , 故 , 故 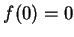 。對 。對 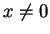 ,
上式最右側為一收斂之幾何級數, 且其和為 ,
上式最右側為一收斂之幾何級數, 且其和為 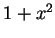 。故
本例與例 1 類似, 雖對 。故
本例與例 1 類似, 雖對
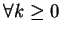 , ,
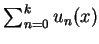 為連續, 但無限個連續函數之和卻不一定仍為一連續函數。
為連續, 但無限個連續函數之和卻不一定仍為一連續函數。
例 6.對
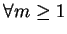 , 令
, 令
是否為一連續函數? 
a
a
進一步閱讀資料:黃文璋(2002).
逐點收斂。微積分講義第八章,國立高雄大學應用數學系。
  
|