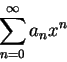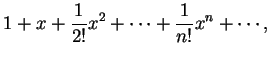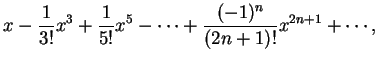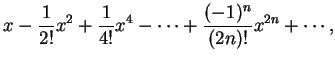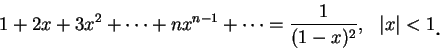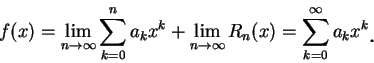前  言

  a

        

　　我們知道若 $\vert x\vert<1$, 則幾何級數 $\sum_{n=0}^{\infty } x^n$ 收歛至 $(1-x)^{-1}$。 即

\begin{displaymath} 1+x+x^2+\cdots+x^n+\cdots=\frac 1{1-x},\ \ \vert x\vert<1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(1.1)

而若 $\vert x\vert\geq 1$, 則上述幾何級數發散。 幾何級數是少數我們可以一簡單的公式來表示其和之收歛級數。 此級數的重要性為, 可由它出發, 而得到許多有趣的級數之和。 

　　這些級數都可視為無限次的多項式, 或稱冪級數 , 也就是它們皆有

\begin{displaymath} \sum_{n=0}^{\infty } a_n x^n \end{displaymath}

的形式, 其中 $a_0$, $a_1,\cdots$, 稱為此冪級數之係數。 較著名的例子有

$\textstyle =$

$\displaystyle 1+x+\frac 1{2!}x^2+\cdots+\frac {1}{n!}x^{n}+\cdots,$  

(1.7)

$\textstyle =$

$\displaystyle x-\frac 1{3!}x^3+\frac 1{5!}x^5-\cdots+\frac {(-1)^n}{(2n+1)!}x^{2n+1}+\cdots,$  

(1.8)

$\textstyle =$

$\displaystyle x-\frac 1{2!}x^2+\frac 1{4!}x^4-\cdots+\frac {(-1)^n}{(2n)!}x^{2n}+\cdots,$  

(1.9)

上述三冪級數的表示法皆對 $\forall x\in R$ 成立。 

　　對冪級數的微分及積分, 我們可如對 (有限次之) 多項式類似的處理。 例如, 將 (1.1) 左、 右分別對 $x$ 微分, 則得

\begin{displaymath} 1+2x+3x^2+\cdots+nx^{n-1}+\cdots=\frac 1{(1-x)^2},\ \ \vert x\vert<1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath} 

(1.10)

　  為什麼許多常見的初等函數皆可表示成冪級數呢 ? 事實上這並不太奇怪, 由第四章定理 3.4 的泰勒公式知, 任一在 0 的一鄰域 $(n+1)$ 次可微的函數, 皆可以一次數不超過 $n$ 的泰勒多項式來逼近。 在 (1.7)$-$(1.9) 中, 那些冪級數的部分和即為泰勒多項式。 當一函數 $f$ 在 0 的一 鄰域之任意階導數皆存在, 則對每一正整數 $n$, 泰勒公式告訴我們, $f$ 可寫成

\begin{displaymath} f(x)=\sum_{k=0}^na_k x^k+R_n(x), \end{displaymath}

(1.15)

其中有限和 $\sum_{k=0}^na_k x^k$ 為一次數不超過 $n$ 之泰勒多項式, 而 $R_n(x)$ 表這種逼近的誤差。 若在 (1.15) 中, 給定 $x$, 而讓 $n$ 趨近 至 $\infty $, 則泰勒多項式趨近至一冪級數 $\sum_{k=0}^{\infty }a_k x^k$, 其中

\begin{displaymath} a_k=f^{(k)}(0)/k!\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

　　若對某些 $x$, 當 $n\to\infty $ 時, 誤差項 $R_n(x)\to 0$, 則對這種 $x$, 在 (1.15) 中, 令 $n\to\infty $, 便得

\begin{displaymath} f(x)=\lim_{n\to\infty }\sum_{k=0}^na_k x^k+\lim_{n\to \infty... ...\sum_{k=0}^{\infty }a_k x^k\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

亦即前述冪級數收歛至。 若一 $x$ 不會使 $\lim_{n\to \infty }R_n(x)=0$, 則部分和 $\sum_{k=0}^na_k x^k$ 便不會趨近至 $f(x)$。 有時並不是那麼容易判斷 $R_n(x)$ 是否趨近至 0, 在那些情況下, 當 $n\to\infty $, $R_n(x)$ 會趨近 至 0, 這將是我們有興趣的課題。 在上一章我們討論了一般級數的收歛性, 那些結果將可協助我們來判別冪級數的收歛性。 

　　比冪級數更一般的, 就是所謂函數級數, 即一級數的每一項 為一函數。 與此相關的就是函數數列 , 本章便要探討函數數列及函數級數。 

　　微分最大的應用之一便是用來協助求一函數的極大值或極小值。許多應用問題中的求最佳解，常可轉換為求一函數的極大值或極小值的問題。
        

　

進一步閱讀資料：黃文璋(2002). 函數數列及函數級數。微積分講義第八章，國立高雄大學應用數學系。