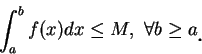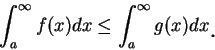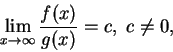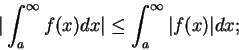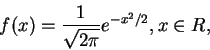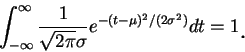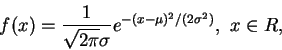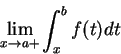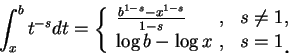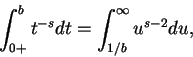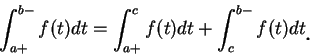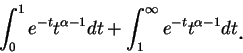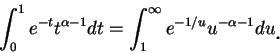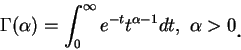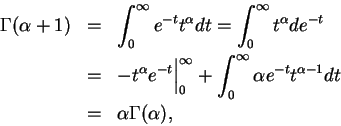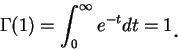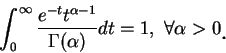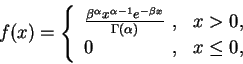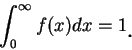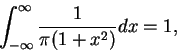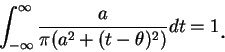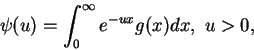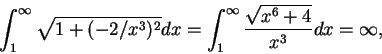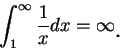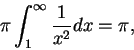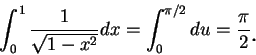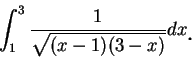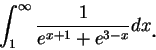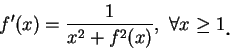7.5瑕積分

瑕積分

在第一章定義積分 $\int_a^b f(x)dx$ 時, 我們做了一些限制, 即函數必須是有界, 且區間為有限。依據那時的分割及求上和與下和的過程, 此二條件乃是必須的。因此那時諸如以下的積分皆沒有定義:

$\begin{displaymath} \int_1^{\infty }\frac 1{x^3}dx,\ \int_{-1}^{1}\frac {\sin x}... ...\int_0^{\infty }\arctan xdx\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

本節我們來看如何放寬此限制, 以擴大可積函數的領域。這就是本節所要介紹的瑕積分 (improper integral, 又稱廣義積分或不正常積分, 之前的積分便稱為正常積分 (proper integral))。

首先, 設對 $\forall b\geq a$ , 積分 $\int_a^b f(x)dx$ 存在。若

$\begin{displaymath} \lim_{b\to\infty }\int_a^bf(x)dx \end{displaymath}$

存在且有限, 則稱 $\int_a^{\infty }f(x)dx$ 收斂, 否則稱為發散, 且寫成

(5.1)

並稱此為第一型之瑕積分 (improper integral of the first kind), 為一無限積分 (infinite integral)。又所謂 $\int_a^{\infty }f(x)dx$ 存在與 $\int_a^{\infty }f(x)dx$ 收斂的意思是相同的。

例 1.考慮瑕積分 $\int_1^{\infty }x^{-s}dx$ 。首先對 $\forall b>1$ ,

$\begin{displaymath} \int_1^b x^{-s}dx=\left\{\begin{array}{lll} \frac {b^{1-s}-1... ...m}, &s=1\mbox{\raisebox{-1.2mm}{\large . }} \end{array}\right. \end{displaymath}$

可看出 $b\to\infty$ 時, 上述積分收斂若且唯若 , 且此時

$\begin{displaymath} \int_1^{\infty } x^{-s}dx=\frac 1{s-1}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

顯然 $\int_1^{\infty }x^{-s}dx$ 的斂散行為類似級數 $\sum_{n=1}^{\infty} n^{-p}$ 。

例 2.因 $b\to\infty$ 時,

$\begin{displaymath} \int_0^b \sin xdx=1-\cos b \end{displaymath}$

之極限並不存在, 故 $\int_0^{\infty } \sin xdx$ 發散。

對第一型的瑕積分, 其收斂與否, 主要是看其尾部。此因
$\int_a^b f(x)dx$ 存在, $\forall b\geq a$ , 故 $\int_a^{\infty }f(x)dx$ 存在, 若且唯若存在一 , 使得 $\int_c^{\infty }f(x)dx$ 存在。又若之反導數存在, 有時會有下述寫法:

$\begin{displaymath} \int_a^{\infty } f(x)dx=F(x)\Big\vert _a^{\infty }=\lim_{x\to\infty }F(x)-F(a)\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

其次, 無限積分 $\int_{-\infty }^bf(x)dx$ 也可類似地定義, 即

$\begin{displaymath} \int_{-\infty }^b f(x)dx=\lim_{a\to -\infty }\int_a^b f(x)dx\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(5.2)

而若存在一 $c\in R$ (注意值並不唯一), 使得 $\int_{-\infty }^c f(x)dx$ 及
皆存在, 則稱收斂, 且其值定義為

$\begin{displaymath} \int^{\infty }_{-\infty } f(x)dx=\int_{-\infty }^c f(x)dx+\int^{\infty }_c f(x)dx\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(5.3)

若上式右側二積分至少有一不存在, 則稱 $\int^{\infty }_{-\infty } f(x)dx$ 發散。值得注意的是 $\int^{\infty }_{-\infty } f(x)dx$ 並不一定等於 $\lim_{b\to\infty }\int_{-b}^bf(x)dx$ 。例如, $\int^{\infty }_{-\infty }\sin xdx$ 為發散, 但 $\lim_{b\to\infty }\int_{-b}^b\sin xdx=0$ 。但若存在, 則其值等於

$\begin{displaymath} \lim_{b\to\infty }\int^b_{-b}f(x)dx \end{displaymath}$ ‧

上述對稱的極限稱為之柯西主值 (Cauchy principal value)。

例 3.考慮瑕積分 $\int_{-\infty }^{\infty }e^{-k\vert x\vert}dx$ 其中。證明它收斂且 $\int_{-\infty }^{\infty }e^{-k\vert x\vert}dx=2/k$ 。

例 4.考慮瑕積分 $\int_{-\infty }^{\infty }1/(1+x^2)dx$ 。證明它收斂且 $\int_{-\infty }^{\infty }1/(1+x^2)dx=\pi$ 。

例 5.令 $S_n=\sum_{j=1}^{n^2}\frac n{n^2+j^2}$ , $n\geq 1$ , 求 $\lim_{n\rightarrow \infty }S_n$ 。

如同在級數中, 對瑕積分亦有一些關於收斂的檢定法。底下為一對積分算子為正時之簡單的檢定法。

定理 1.設 $f(x)\geq 0$ , $\forall x\geq a$ , 又設對 $\forall b\geq a$ , $\int_a^b f(x)dx$ 皆存在。則
$\int_a^{\infty }f(x)dx$ 收斂, 若且唯若存在一 , 使得

$\begin{displaymath} \int_a^b f(x)dx\leq M,\ \forall b \geq a\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

定理 2.(比較檢定法)設對 $\forall x\geq a$ , $0\leq f(x)\leq g(x)$ 。又設 $\int_a^b f(x)dx$ 存在, $\forall b\geq a$ , 且 $\int_a^{\infty }g(x)dx$ 收斂. 則 $\int_a^{\infty }f(x)dx$ 收斂, 且

$\begin{displaymath} \int_a^{\infty } f(x)dx\leq \int_a^{\infty }g(x)dx\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

在上定理中, 我們稱 $\int_a^{\infty }g(x)dx$ 支配 $\int_a^{\infty }f(x)dx$ 。由於 $f(x)\geq 0$ , 故 $\int_a^b f(x)dx$ 為一之增函數。又因 $f(x)\leq g(x)$ , 故

$\int_a^b f(x)dx\leq \int_a^bg(x)dx\leq\int_a^{\infty }g(x)dx<\infty$ 。

故定理 5.2 亦為一種單調且有界的數列必收斂的結果。

定理 3.(極限比較檢定法)設對 $\forall x\geq a$ , $f(x)\geq 0$ , 。又設對 $\forall b\geq a$ , $\int_a^b f(x)dx$ 及 $\int_a^bg(x)dx$ 皆存在。若

$\begin{displaymath} \lim_{x\to\infty }\frac {f(x)}{g(x)}=c,\ c\neq 0, \end{displaymath}$

(5.4)

則 $\int_a^{\infty }f(x)dx$ 及 $\int_a^{\infty }g(x)dx$ 同時收斂或發散。若 , 則 $\int_a^{\infty }g(x)dx$ 收斂導致 $\int_a^{\infty }f(x)dx$ 收斂。而若 $c=\infty$ , 則 $\int_a^{\infty }g(x)dx$ 發散導致
$\int_a^{\infty }f(x)dx$ 發散。

定理 4.

(i) 對 $\forall a\in R\cup \{-\infty \}$ , 若 $\int_a^{\infty }\vert f(x)\vert dx$ 收斂, 則 $\int_a^{\infty }f(x)dx$ 收斂, 且

$\begin{displaymath} \vert\int_a^{\infty }f(x)dx\vert\leq \int_a^{\infty }\vert f(x)\vert dx; \end{displaymath}$

(ii) 若 $f(x)\geq 0$ , $\forall x\geq 0$ , $f(x)\leq 0$ , $\forall x<0$ , 則 $\int_{-\infty }^{\infty } f(x)$ 收斂, 若且唯若 $\int_{-\infty }^{\infty }\vert f(x)\vert dx$ 收斂。

若 $\int_a^{\infty }f(x)dx$ 收斂, 則 $\int_a^{\infty }\vert f(x)\vert dx$ 不一定收斂。故定理 4 為一值得留意及比較的結果。

例 6.討論 $\int_1^{\infty } x/(3x^2+4x+5)dx$ 及 $\int_1^{\infty } x^2/(x^4+5x+6)dx$ 之斂散性。

例 7.考慮瑕積分 $\int_0^{\infty } e^{-x^2/2}dx$ 。證明它存在。

一函數若滿足 $g(x)\geq 0$ , $\forall x\in R$ , 且 $\int_{-\infty }^{\infty }g(x)dx=1$ , 則稱為一機率密度函數。故若令

$\begin{displaymath} f(x)=\frac 1{\sqrt {2\pi}}e^{-x^2/2}, x\in R, \end{displaymath}$

(5.6)

則為一機率密度函數。對一收斂的瑕積分, 變數代換仍適用。若令 $x=(t-\mu)/\sigma$ , 則得

$\begin{displaymath} \int_{-\infty }^{\infty }\frac 1{\sqrt {2\pi}\sigma}e^{-(t-\mu)^2/(2\sigma^2)}dt=1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

故對 $\forall \mu\in R$ , $\sigma>0$ ,

$\begin{displaymath} f(x)=\frac 1{\sqrt {2\pi}\sigma}e^{-(x-\mu)^2/(2\sigma^2)},\ x\in R, \end{displaymath}$

(5.7)

仍為一機率密度函數。誤差理論是高斯對機率論的主要貢獻。高斯發現 (5.7) 式定義出之機率密度函數, 在誤差理論中扮演著一極重要的角色。

例 8. 證明 $\int_1^{\infty }e^{-x}x^sdx$ 收斂。

設一函數定義在 , 且對 $\forall x\in (a, b]$ , $\int_x^b f(t)dt$ 存在。則 $\int_{a+}^bf(t)dt$ 稱為第二型之瑕積分 , 且若

$\begin{displaymath} \lim_{x\to a+}\int_x^bf(t)dt \end{displaymath}$

存在且有限, 則稱此瑕積分收斂, 否則稱為發散。此時並定義

例 9.對 $\forall b>x>0$ ,

$\begin{displaymath} \int_x^b t^{-s}dt=\left\{\begin{array}{lll} \frac {b^{1-s}-x... ...m}, &s=1\mbox{\raisebox{-1.2mm}{\large . }} \end{array}\right. \end{displaymath}$

當 $x\to 0+$ 上述積分存在, 若且唯若。故 $\int_{0+}^b t^{-s}dt$ 存在, 若且唯若。

　　另外, 經由之變換, 可得

當 $x\to 0+$ , $1/x\to\infty$ , 因此

$\begin{displaymath} \int_{0+}^b t^{-s}dt=\int_{1/b}^{\infty }u^{s-2}du, \end{displaymath}$

只要上式右側積分存在。而由例 1 知, 上式右側積分存在, 若且唯若 , 即。

例 10.求 $\int_{0+}^1 x\log xdx$ 。

例 9 顯示, 第二型之瑕積分可化為第一型之瑕積分, 所以我們並不需特別列出關於第二型之瑕積分的檢定法。

我們也可類似地定義瑕積分 $\int_a^{b-}f(t)dt$ 。又若 $\int_{a+}^c f(t)dt$ 與
$\int_c^{b-}f(t)dt$ 皆收斂, 則定義

$\begin{displaymath} \int_{a+}^{b-}f(t)dt=\int_{a+}^{c}f(t)dt+\int_c^{b-}f(t)dt\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

有時為了簡便, 往往以 $\int_a^{b}f(t)dt$ 取代 $\int_{a+}^{b-}f(t)dt$ 或 $\int_{a+}^{b}f(t)dt$ 或
$\int_a^{b-}f(t)dt$ 。

瑕積分的定義可以再稍加推廣。例如, 若在 , 皆無定義, 其中 , 則若 $\int_a^{c-}f(t)dt$ , $\int_{c+}^{d-}f(t)dt$ , $\int_{d+}^{b}f(t)dt$ 皆收斂, 便稱 $\int_a^{b}f(t)dt$ 收斂, 且以此三積分之和當做 $\int_a^{b}f(t)dt$ 之定義。另外, 也可有兩類型瑕積分之混合。例如, 考慮 $\int_{a+}^{b}f(t)dt+\int_b^{\infty } f(t)dt$ , 且以 $\int_{a+}^{\infty }f(t)dt$ 或 $\int_a^{\infty }f(t)dt$ 表此混合型的瑕積分。

例 11.底下我們來判別 $\int_0^{\infty }\sin x/xdx$ 之斂散性, 此積分稱為
Dirichlet 積分 , 曾為 Dirichlet 所探討。

$\int_0^{\infty }\sin x^2dx$ 及 $\int_0^{\infty }\cos x^2dx$ 稱為 Fresnel 積分, 出現於光線的繞射原理。由 Fresnel 積分知, 即使 $\lim_{x\to\infty }f(x)\neq 0$ , $\int_{0}^{\infty }f(x)dx$ 仍有可能收斂, 這是與級數的收斂不同的地方。事實上, 即使不為有界, $\int_0^{\infty }f(x)dx$ 仍可能收斂。例如, 考慮 $\int_0^{\infty }2u\cos u^4du$ 。當 $\sqrt [4]{n\pi}$ , , , $2,\cdots$ , 積分算子成為 $2\sqrt [4]{n\pi}\cos n\pi=2\sqrt [4]{n\pi}$ 或 $-2\sqrt [4]{n\pi}$ , 故積分算子不為有界。但若令 , 則此積分成為 $\int_0^{\infty }\cos x^2dx$ 為收斂。

例 12.由例 2 知 $\int_0^{\infty } \sin xdx$ 發散, 證明 $\int_0^{\infty }\sin x^2dx$ 收斂。

　　接著我們介紹一在應用數學中極重要的 gamma 函數。

例 13.設 $\alpha >0$ , 底下證明 $\int_0^{\infty }e^{-t}t^{\alpha -1}dt$ 收斂。先將此積分改寫為

$\begin{displaymath} \int_0^{1}e^{-t}t^{\alpha -1}dt+\int_1^{\infty }e^{-t}t^{\alpha -1}dt\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

其中第二個積分已在例 8 中知道收斂。至於第一個積分, 令 , 則

$\begin{displaymath} \int_0^{1}e^{-t}t^{\alpha -1}dt=\int_1^{\infty }e^{-1/u}u^{-\alpha -1}du\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

但只要與 $\int_1^{\infty }u^{-\alpha -1}du$ 比較便知 $\int_1^{\infty }e^{-1/u}u^{-\alpha -1}du$ 收斂, $\forall \alpha >0$ 。因此 $\int_0^{1}e^{-t}$ $t^{\alpha -1}dt$ 收斂, $\forall \alpha >0$ 。故當 $\alpha >0$ 時 $\int_0^{\infty }e^{-t}t^{\alpha -1}dt$ 收斂。我們便定義一新函數

$\begin{displaymath} \Gamma (\alpha )=\int_0^{\infty }e^{-t}t^{\alpha -1}dt,\ \alpha >0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(5.8)

$\Gamma$ 稱為 gamma 函數, 此函數有一些有趣的性質。如對 $\forall \alpha >0$ ,

$\begin{eqnarray*} \Gamma (\alpha +1) &=& \int_0^{\infty }e^{-t}t^{\alpha }dt =\i... ... }\alpha e^{-t} t^{\alpha -1}dt \\ &=& \alpha \Gamma (\alpha ), \end{eqnarray*}$

即

$\begin{displaymath} \Gamma (\alpha +1)=\alpha \Gamma (\alpha ),\ \forall \alpha >0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(5.9)

又

$\begin{displaymath} \Gamma (1)=\int_0^{\infty }e^{-t}dt=1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(5.10)

由 (5.9) 及 (5.10) 即得對每一正整數 ,

$\begin{displaymath} \Gamma (n+1)=n!\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(5.11)

又利用 (5.5) 可得

$\begin{displaymath} \Gamma(\frac 1 2)=\sqrt {\pi}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(5.12)

再利用 (5.9) 即得

$\begin{displaymath} \Gamma(\frac 3 2)=\Gamma(\frac 1 2+1)=\frac 1 2\Gamma(\frac 1 2)=\frac {\sqrt {\pi}}2\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

同理對每一正整數 , 皆可求出 $\Gamma(n/2)$ 。

由 (5.8) 式得

$\begin{displaymath} \int_0^{\infty }\frac {e^{-t}t^{\alpha -1}}{\Gamma (\alpha )}dt=1,\ \forall \alpha >0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

若變數代換, 令 $t=\beta x$ , 其中 $\beta >0$ 為一常數, 則得

$\begin{displaymath} \int_0^{\infty }\frac {e^{-\beta x}(\beta x)^{\alpha -1}}{\G... ...a x}}{\Gamma (\alpha )}dx=1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

故若令

$\begin{displaymath} f(x)=\left\{\begin{array}{lll} \frac {\beta ^{\alpha }x^{\al... ... & x>0, \\ 0 &\hspace{-0.2cm}, & x \leq 0, \end{array}\right. \end{displaymath}$

(5.13)

其中 $\alpha$ , $\beta$ 為二正的常數, 則 , $\forall x>0$ ,且

$\begin{displaymath} \int_0^{\infty }f(x)dx=1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(5.13) 定義之函數亦為一重要的機率密度函數。另外,由例 4 知, 若令

$\begin{displaymath} h(x)=\frac 1{\pi(1+x^2)},\ x\in R, \end{displaymath}$

(5.14)

則因

$\begin{displaymath} \int_{-\infty }^{\infty }\frac 1{\pi (1+x^2)}dx=1, \end{displaymath}$

故亦為一機率密度函數。再利用變數代換, 令 $x=(t-\theta)/a$ , 得

$\begin{displaymath} \int_{-\infty }^{\infty }\frac a{\pi (a^2+(t-\theta)^2)}dt=1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

故對 $\forall a>0$ , $\theta\in R$ ,

$\begin{displaymath} f(x)=\frac a{\pi (a^2+(x-\theta)^2)},\ x\in R, \end{displaymath}$

(5.15)

此為一常見的機率密度函數。

其次來看 Lalpace 轉換 (Laplace transform)。設一函數定義在 $[0,\infty )$ 上, 且 $g(x)\geq 0$ , $\forall x\geq 0$ 。則

$\begin{displaymath} \psi(u)=\int_{0}^{\infty }e^{-ux}g(x)dx,\ u>0, \end{displaymath}$

(5.16)

稱為之 Laplace 轉換, 只要上述積分存在。

若之定義如 (5.13), 則之 Lalpace 轉換為

$\begin{eqnarray*} \psi(u)&=&\int_{0}^{\infty }e^{-ux}\frac {\beta ^{\alpha }x^{\... ...pha )}dx \\ &=&\left(\frac {\beta }{\beta +u}\right)^{\alpha }, \end{eqnarray*}$

此處用到最後一積分中的積分算子亦有 (5.13) 式中之的形式, 只是 $\beta$ 改為 $\beta +u$ , 故其積分仍為 1。

例 14.設有一函數 $f(x)=1/x^2, x\geq 1$ 。則此函數圖形之弧長為

$\begin{displaymath} \int_1^{\infty }\sqrt {1+(-2/x^3)^2}dx=\int_1^{\infty }\frac {\sqrt {x^6+4}}{x^3}dx=\infty , \end{displaymath}$

此因 $\lim_{x\to\infty }\sqrt {x^6+4}/x^3=1\neq 0$ 。但之圖形下由 1 至 $\infty$ 之面積為

$\begin{displaymath} \int_1^{\infty }\frac 1{x^2}dx=\left.-\frac 1 x\right\vert _1^{\infty }=1, \end{displaymath}$

為一有限值。

另外, 令 $g(x)=1/x, x\geq 1$ , 則之圖形下由 1 至 $\infty$ 之面積為

$\begin{displaymath} \int_1^{\infty }\frac 1 xdx=\infty \mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

但之圖形繞軸旋轉所圍之體積為

$\begin{displaymath} \pi\int_1^{\infty }\frac 1{x^2}dx=\pi, \end{displaymath}$

為一有限值。

經由變數代換, 一瑕積分有時可轉換為一正常積分。例如, 若令 $x=\sin u$ , 則

$\begin{displaymath} \int_0^1\frac 1{\sqrt {1-x^2}}dx=\int_0^{\pi/2}du=\frac {\pi} 2\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

另一方面, 一連續函數的積分也有可能轉換成一瑕積分。這種情況發生在若令 $u=\phi(x)$ , 且在積分區間的端點, 導數 $\phi'(x)$ 為 0, 故為無限大。

例 15.求

$\begin{displaymath} \int_1^3\frac 1{\sqrt {(x-1)(3-x)}}dx\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

例 16.求

$\begin{displaymath} \int_1^{\infty }\frac 1{e^{x+1}+e^{3-x}}dx\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

例 17.設為一可微函數, 且 , 又

$\begin{displaymath} f'(x)=\frac 1{x^2+f^2(x)},\ \forall x\geq 1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(5.17)

試證 $\lim_{x\to\infty }f(x)$ 存在且極限值小於 $1+\pi/4$ 。

例 18.設函數定義在 $x\geq 0$ , 其函數圖形如圖 5.1。

一般而言且 , $n\geq 0$ , 且圖形由一些等腰三角形所組成, 並對稱於軸。則 $\int_0^{\infty }f(x)dx$ 收斂且其值為 0, 但 $\int_0^{\infty }\vert f(x)\vert dx$ 發散。若修改 , 使其函數圖形中的等腰三角形, 底部長度依序為 1, 1, 1/2, 1/2, 1/3, 1/3, $\cdots$ , 而三角形之高維持為 1, 而得一函數 , 則此亦為一 $\lim_{x\to\infty }g(x)\neq 0$ 但 $\int_0^{\infty } g(x)dx$ 收斂之例。

$\begin{picture}(0,150)(-40,0)\thicklines\put(-20,55){\vector(1,0){300}} \put(0,0... ...(50,5){$-1$} \put(130,24){$-\frac 1 2$} \put(210,30){$-\frac 1 3$} \end{picture}$

圖 5.1.

進一步閱讀資料：黃文璋(2002). 數列及級數。微積分講義第七章，國立高雄大學應用數學系。
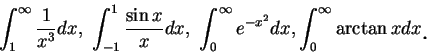
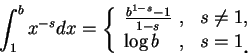
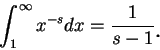
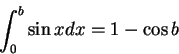
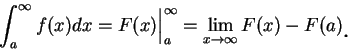
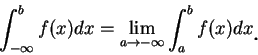
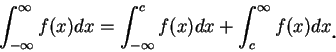
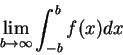