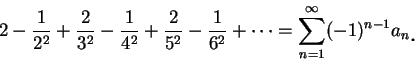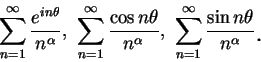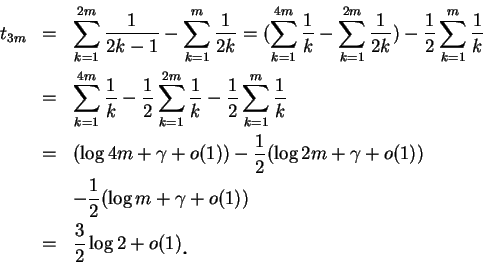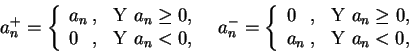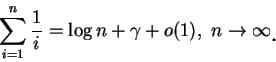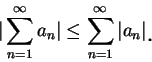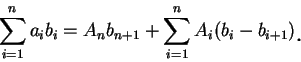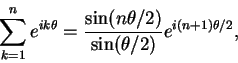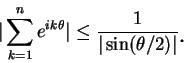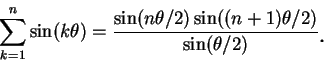交錯級數
交錯級數 (alternating series), 即一正、負項交錯的級數,
其形式為
其中  。
。下述定理為萊布尼茲規則
(Leibniz rule)。
例 1.由於數列
 漸減至 0, 故交錯級數
漸減至 0, 故交錯級數
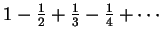 收斂。本例顯示,
即使
收斂。本例顯示,
即使 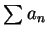 及
及 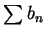 皆發散, 但
皆發散, 但
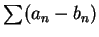 卻有可能收斂, 在此
卻有可能收斂, 在此 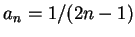 ,
, 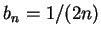 ,
,
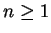 。
。
例 2.級數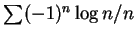 收斂或發散。
收斂或發散。
例 3.(i)試證級數
收斂,
並估計其和 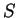 至小數第 3 位。
至小數第 3 位。
(ii)討論級數
之斂散性。
例 4.(i)討論級數
之斂散性。
(ii)討論級數
之斂散性。
不過要注意的是, 定理 1
只是提供一判斷交錯級數是否收斂之充分條件.。即使不滿足定理
1 中的條件, 交錯級數
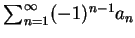 仍有可能收斂。
仍有可能收斂。
例 5.利用萊布尼茲規則可導出一重要的極限結果。令
一般項為
易見
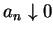 , 故交錯級數
, 故交錯級數
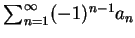 收斂。若以
收斂。若以 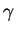 表此級數和, 而至第
表此級數和, 而至第 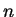 項之部分和為
項之部分和為 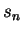 , 則
因
, 則
因 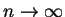 時,
時,
 , 故得
, 故得
|
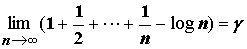
|
(4.2) |
常數 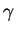 稱為歐拉常數 (Euler's
constant)。
稱為歐拉常數 (Euler's
constant)。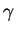 為一 重要的常數, 其值約為 0.5772156649。(4.2)
又可表示為
為一 重要的常數, 其值約為 0.5772156649。(4.2)
又可表示為
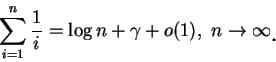 |
(4.3) |
由此即得
因此又有
由 (4.3) 不但再度可看出為何調和級數 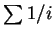 發散, 也可看出
發散, 也可看出
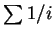 成長之速度。
成長之速度。
例 6.求

之和。
例 7.試判斷級數
之斂散性。
一般而言, 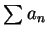 收斂不一定導致
收斂不一定導致 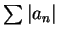 收斂。不過若
收斂。不過若 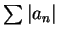 收斂卻可導出
收斂卻可導出 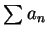 收斂。
收斂。
例 8.級數
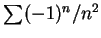 、
、
 及
及
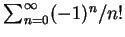 皆為絕對收斂, 而
皆為絕對收斂, 而
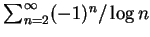 為條件收斂。
為條件收斂。
例 9.證交錯級數
為絕對收斂。
下述定理稱為Abel 部分和公式
(Abel partial summation formula)。
由 (4.5) 可看出, 當 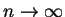 時, 若級數
時, 若級數
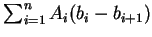 及數列
及數列
 皆收斂, 則
皆收斂, 則 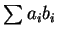 收斂。底下兩個定理即給出前述級數及數列收斂之充分條件,
因此亦為
收斂。底下兩個定理即給出前述級數及數列收斂之充分條件,
因此亦為 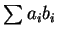 收斂之一充分條件。
收斂之一充分條件。
在定理 5 及 6 中, 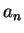 皆可為複數。 一複數數列
皆可為複數。 一複數數列 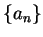 收斂, 若且唯若其實部數列及虛部數列皆收斂,
且
收斂, 若且唯若其實部數列及虛部數列皆收斂,
且 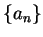 極限為其實部數列與虛部數列之極限和。而一類重要的發散級數,
但部分和為有界的級數為幾何級數
極限為其實部數列與虛部數列之極限和。而一類重要的發散級數,
但部分和為有界的級數為幾何級數 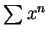 , 其中
, 其中 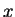 為一複數且
為一複數且
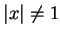 。由此定理也可導出第二章之
(5.3) 式。首先注意到若
。由此定理也可導出第二章之
(5.3) 式。首先注意到若 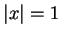 , 則
, 則
 , 其中
, 其中 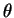 為一實數,
為一實數,  , 而
, 而
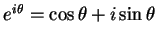 。
。
設 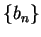 為一漸減至 0 之實數列, 且取
為一漸減至 0 之實數列, 且取 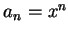 , 其中
, 其中 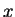 為一複數, 且
為一複數, 且 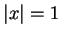 ,
, 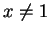 。則由定理 5 及 7 知
。則由定理 5 及 7 知
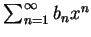 收斂。定理 1 為此結果當
收斂。定理 1 為此結果當 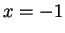 之一特例。
之一特例。
現取  , 其中
, 其中  且不為
且不為 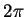 之整數倍。考慮級數
之整數倍。考慮級數
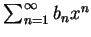 , 則其實部
, 則其實部
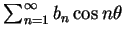 與虛部
與虛部
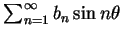 皆收斂。特別地,
若取
皆收斂。特別地,
若取
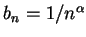 ,
, 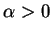 , 則下述級數皆收斂:
, 則下述級數皆收斂:
又當 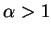 , 上述各級數因皆受制於
, 上述各級數因皆受制於
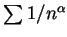 , 故皆絕對收斂。
, 故皆絕對收斂。
附帶一提, 因在 (4.6) 兩側實部及虛部須各自相等, 故得
|

|
(4.8) |
及
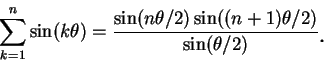 |
(4.9) |
不難看出 (4.8) 式與第二章 (5.3) 式是相同的。
在例 8 我們證明了
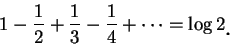 |
(4.10) |
但若將此級數重排, 先寫兩正項再寫一負項, 則得下述新級數:
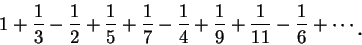 |
(4.11) |
此新級數與原交錯調和級數的各項有 1 1 且映成的關係,
但可如下地證明其和 卻不為
1 且映成的關係,
但可如下地證明其和 卻不為 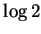 。
。
令 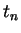 表 (4.11) 之級數至第
表 (4.11) 之級數至第 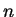 項的部分和。則對
項的部分和。則對  ,
因包含
,
因包含  個 正項及
個 正項及 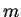 個負項, 故利用 (4.3), 得
個負項, 故利用 (4.3), 得
故
又因
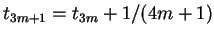 ,
,
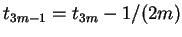 , 故
故得
, 故
故得
由上例可看出將一收斂級數重排後, 可能得到一不同的和。此現象只有對條件收斂的級數才會發生。也就是一絕對收斂的級數雖經重排也不會改變其和。
在上述定理中, 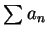 為絕對收斂乃必要的。Riemman 發現,
對一條件收斂的級數, 只要經適當的重排, 可讓其和收斂至任一給定的實數。 Riemann 之證明,
用到條件收斂級數之一特性, 即必有無限多個正項及無限多個負項
(否則就是絕對收斂了)。若令
為絕對收斂乃必要的。Riemman 發現,
對一條件收斂的級數, 只要經適當的重排, 可讓其和收斂至任一給定的實數。 Riemann 之證明,
用到條件收斂級數之一特性, 即必有無限多個正項及無限多個負項
(否則就是絕對收斂了)。若令
即
則 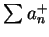 與
與 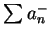 分別為
分別為 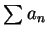 之正項及負項部分, 而且
此二級數與
之正項及負項部分, 而且
此二級數與  有下述關係。
有下述關係。
例如, 對級數
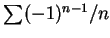 , 此級數為條件收斂, 且對應的
, 此級數為條件收斂, 且對應的
 ,
, 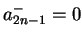 ,
, 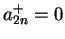 ,
,
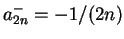 。顯然
。顯然 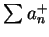 及
及 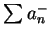 皆發散。但對
皆發散。但對
 , 此級數為絕對收斂, 易見對應的
, 此級數為絕對收斂, 易見對應的 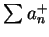 及
及 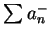 皆收斂。
皆收斂。
最後我們證明 Riemann 重排定理 (Riemann's Rearrangement
Theorem) 。
進一步閱讀資料:黃文璋(2002).
數列及級數。微積分講義第七章,國立高雄大學應用數學系。
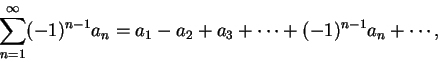

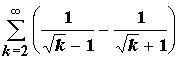
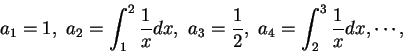
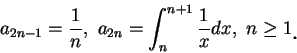
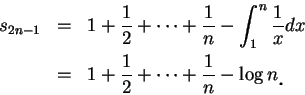
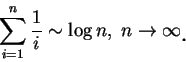
![\begin{displaymath}
\frac 1 3+\frac 1{3\sqrt {3}}+\frac 1{3\sqrt {3}\sqrt [3]{3}...
...dots
+\frac 1{3\sqrt {3}\sqrt [3]{3}\cdots\sqrt [n]{3}}+\cdots
\end{displaymath}](img88.gif)