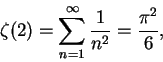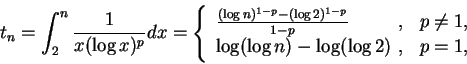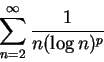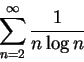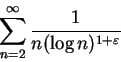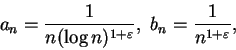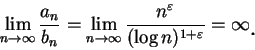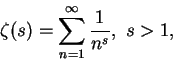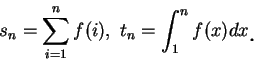|
  
正項級數
設有一級數  , 若 , 若 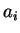 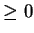 , , 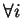 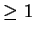 , 稱此為一正項級數 (positive term series, 或 nonnegative term
series)。對一正項級數, 因部分和 , 稱此為一正項級數 (positive term series, 或 nonnegative term
series)。對一正項級數, 因部分和
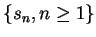 為一漸增數列, 利用第一章定理 1.1
便得底下的結果。 為一漸增數列, 利用第一章定理 1.1
便得底下的結果。
|
定理
1.設  為一正項級數。則 為一正項級數。則  收斂, 若且唯若 部分和數列有上界。 收斂, 若且唯若 部分和數列有上界。
|
理論上來說,
欲判別一級數之斂散性, 須檢驗其部分和數列
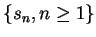 是否極限存在。但很多時候 是否極限存在。但很多時候 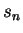 並無簡單的形式, 因此也就不易看出
並無簡單的形式, 因此也就不易看出 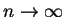 時, 時, 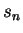 之 極限值是否存在。利用下列方法可不經由求部分和即可來判別。 之 極限值是否存在。利用下列方法可不經由求部分和即可來判別。
級數之斂散性的判別法有三大類: (i) 充分條件,
(ii) 必要條件, (iii)
充要條件。設 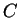 為關 於級數 為關 於級數  之某一條件, 則上述三類分別可如下說明: 之某一條件, 則上述三類分別可如下說明:
(i) 若 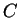 成立, 則 成立, 則  收斂; 收斂;
(ii) 若  收斂, 則 收斂, 則 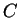 成立; 成立;
(iii)  收斂, 若且唯若 收斂, 若且唯若 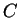 成立。 成立。 例 1.
設  為一重疊級數, 為一重疊級數,
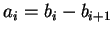 , 則 , 則
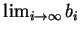 存在, 為 存在, 為  收斂之一充分條件。而 收斂之一充分條件。而
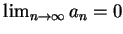 為 為  收斂之一 必要條件。又若已知 收斂之一 必要條件。又若已知
 為一等比級數, 則公比小於 1 為此級數收斂的充要條件。對必要條件,
可用來判別級數發散, 即若 為一等比級數, 則公比小於 1 為此級數收斂的充要條件。對必要條件,
可用來判別級數發散, 即若
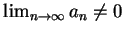 , 則此級數發散。 , 則此級數發散。
本節先討論關於正項級數之斂散性的判別法。
在定理 2之條件下,
一個等價的結果為若  發散, 則 發散, 則 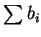 發散。而若存在一 發散。而若存在一 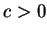 , 使得 (3.1) 成立, 我們便說級數 , 使得 (3.1) 成立, 我們便說級數
 受制於 受制於 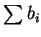 ( ( is dominated by is dominated by 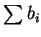 ), 或說 ), 或說 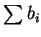 支配 支配  。 又顯然若存在一 。 又顯然若存在一 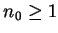 , 使得 (3.1) 成立, , 使得 (3.1) 成立,
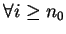 , 則上定理 2之結果仍成立。甚至,
若 , 則上定理 2之結果仍成立。甚至,
若 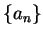 及 及 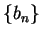 是自某項開始為非負, 則定理 3.2 之結果仍成立。一級數之斂散性,
不受前面有限項的影響。 是自某項開始為非負, 則定理 3.2 之結果仍成立。一級數之斂散性,
不受前面有限項的影響。
註 3.1. 若存在一常數 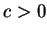 , 使得 , 使得
亦即
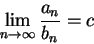 |
(3.3) |
時, 由定理 3 知此時 與 與 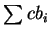 同時收斂或發散。故當
(3.3) 成立時, 同時收斂或發散。故當
(3.3) 成立時,  收斂若且唯若 收斂若且唯若 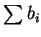 收斂。另外, 若 收斂。另外, 若 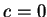 , 則易見此時只能得到結論: , 則易見此時只能得到結論: 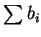 收斂 導致 收斂 導致
 收斂, 而 收斂, 而  發散導致 發散導致 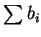 發散。最後, 若 發散。最後, 若 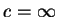 , 則 , 則 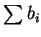 發散導致 發散導致  發散, 發散,  收斂導致
收斂導致 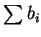 收斂。 收斂。
由定理 3 即得下述推論。
例 2.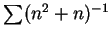 為一收斂的重疊級數。因 為一收斂的重疊級數。因
故由系理 1 知 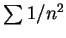 收斂。又對 收斂。又對 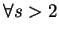 , , 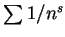 受制於 受制於 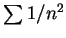 。 。
故 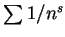 收斂, 收斂,
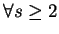 。稍後會證明, 事實上 。稍後會證明, 事實上 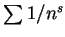 收斂, 收斂, 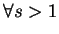 。 。
若令
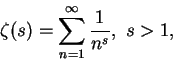 |
(3.4) |
便定義出著名的
Riemann zeta 函數 (Riemann
zeta-function, 簡稱
zeta 函數)。歐拉發現許多關於 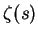 之美妙的公式, 例如,
之美妙的公式, 例如,
此公式至 8.6
節再推導。
例 3. (i)討論級數
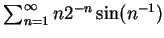 之斂散性。 之斂散性。
(ii)討論級數
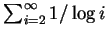 之斂散性。 之斂散性。
(iii)討論級數 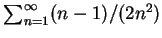 之斂散性。 之斂散性。

利用底下柯西在西 元 1837 年證明的積分檢定法 (integral test),
可判別更多級數的斂散性。
例 4.對 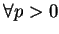 , 級數 , 級數
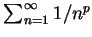 稱為一 稱為一 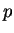 級數 ( 級數 (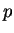 series)。在例 2. 已證明 series)。在例 2. 已證明 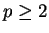 時, 此級數收斂。如何利用積分檢定法,
證明此級數收斂, 若且唯若 時, 此級數收斂。如何利用積分檢定法,
證明此級數收斂, 若且唯若 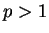 。 。
例 5.試判別
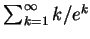 之斂散性。 之斂散性。
例 6.因
故 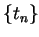 收斂若且唯若 收斂若且唯若 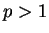 , 因此 , 因此
收斂若且唯若 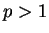 。我們知道 。我們知道 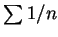 發散, 而只要 發散, 而只要 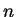 的次方比 1 大, 譬如說 的次方比 1 大, 譬如說
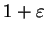 , 其中 , 其中 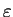 可以是一任意小的固定正數, 則
收斂。上例指出, 事實上分母可``更小些". 此因雖
發散, 而
收斂, 其中 可以是一任意小的固定正數, 則
收斂。上例指出, 事實上分母可``更小些". 此因雖
發散, 而
收斂, 其中 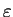 可為一任意小之固定正數。而若令
則 可為一任意小之固定正數。而若令
則
對二正項級數 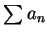 與 與 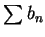 , 且 , 且
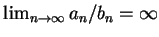 ,
則由 ,
則由 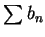 收斂並無法確定 收斂並無法確定 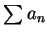 是否收斂。本例即指出,
雖級數 是否收斂。本例即指出,
雖級數 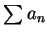 比 比 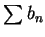 “大很多”, 但 “大很多”, 但 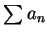 仍有可能收斂。這種例子其實很多, 如取
仍有可能收斂。這種例子其實很多, 如取 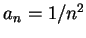 , , 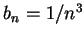 ,
則 ,
則
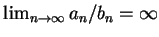 , 但 , 但 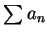 與 與 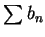 皆收斂。 皆收斂。
關於正項級數尚有兩種常用的檢定收斂的方法。
(i)根式檢定法 (root test).
例 7.分別討論下述各級數
之斂散性。
(ii)比值檢定法 (ratio test)。
|
定理
6.設有一級數 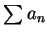 , 自第某項開始 , 自第某項開始 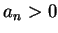 , 且滿足 , 且滿足

(i) 若 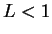 , 則級數收斂; , 則級數收斂;
(ii) 若 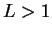 , 則級數發散; , 則級數發散;
(iii) 若 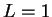 , 則此法失效。 , 則此法失效。
|
對一級數 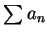 , 即使 , 即使 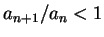 , ,
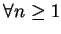 , 也不保證此級數收斂。因此時 , 也不保證此級數收斂。因此時
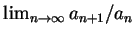 仍有可能為
1。例如, 若 仍有可能為
1。例如, 若 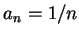 , 則 , 則
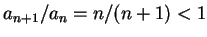 , ,
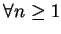 , 但 , 但 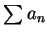 發散。不過若 發散。不過若 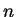 夠大時 夠大時 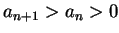 , 則 , 則
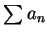 必發散, 因此時 必發散, 因此時 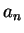 不趨近至 0。 不趨近至 0。
例 8.討論下述各級數的斂散性。
(i)
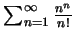 ; ;
(ii)
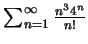 ; ;
(iii)
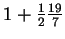
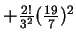
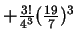 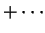 . .
例 9.討論下述各級數的斂散性, 其中 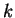 為一常數。 為一常數。
(i)
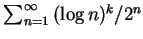 , ,
(ii)
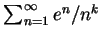 . .
一級數之收斂或發散是確定的,
某一方法失效, 不表示此級數之斂散性不能決定。一般而言,
比值檢定法較根式檢定法好用。但是根式檢定法適用性較廣。更明確地說,
當由比值檢定法證出級數收斂時,
由根式檢定法亦可得到級數收斂;
而當根式檢定法失效時, 比值檢定法亦失效。底下便給一比值檢定法失效但根式檢定法成功的例子。
例 10.設有一級數
則
故
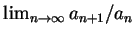 不存在, 因此比值檢定法失效。 不存在, 因此比值檢定法失效。
但
故由根式檢定法知此級數收斂。
進一步閱讀資料:黃文璋(2002).
數列及級數。微積分講義第七章,國立高雄大學應用數學系。
  
|