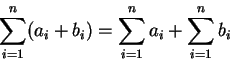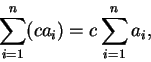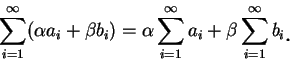|
級數的基本性質
一級數若有下述形式, 便稱為一公比為 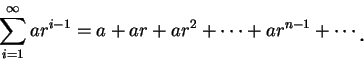
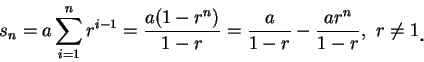
對每一數列
設一數列
由以上討論即得下述定理。
故由定理知, 數列
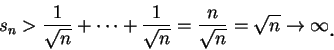
故此級數發散。 不過當然並非每一發散級數, 其部分和必趨近至 或 對每一整數
對每一 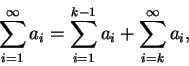
而有限個和
其次, 我們看級數的線性性質。首先對有限個數的和,
有底下二簡單但重要的性質:
及
下述定理指出, 對二收斂級數仍有線性的性質。
至於若
若有一級數
則稱此為重疊級數(telescoping series)。我們有下述定理。
且
|
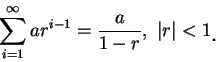
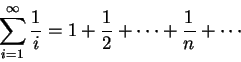 稱為調和級數 (harmonic series)。因對
,
稱為調和級數 (harmonic series)。因對
,
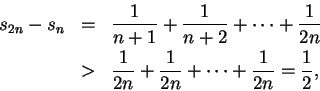
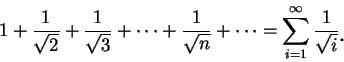 當
當