|
  
前言
a
設有一數列
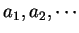 。依序求其部分和,
可得數列 。依序求其部分和,
可得數列
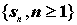 , 其中
, 其中
當 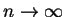 , 便得到和 , 便得到和
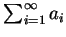 , 此稱為一無限級數
(infinite series), 或只簡稱級數
(series). 反之, 設有一級數
, 此稱為一無限級數
(infinite series), 或只簡稱級數
(series). 反之, 設有一級數
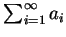 , 則其部分和 , , 則其部分和 ,
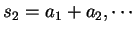 ,
亦構成一數列. 若
其中 ,
亦構成一數列. 若
其中 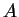 為一實數, 則稱級數 為一實數, 則稱級數
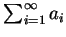 收歛, 且 收歛, 且 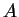 稱為此收歛級數之和, 否則稱為發散。 一發散級數之和並不存在。 在
稱為此收歛級數之和, 否則稱為發散。 一發散級數之和並不存在。 在
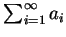 中, 中,
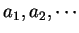 稱為級數的項, 而 稱為級數的項, 而 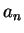 稱為第
稱為第 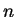 項或一般項 (general term)。 項或一般項 (general term)。 首先若一數列
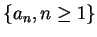 收歛到一有限的值 收歛到一有限的值 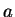 , 則當 , 則當 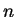 很大時, 很大時, 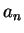 與
與 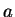 之 差距將很小。因此, 若 之 差距將很小。因此, 若 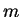 與 與 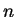 皆很大, 則 皆很大, 則 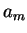 與 與
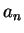 之差距亦很小。也就是只要項數夠大, 則任兩項可任意接近。正式地說, 我們有下述定理。 之差距亦很小。也就是只要項數夠大, 則任兩項可任意接近。正式地說, 我們有下述定理。
由上述定理即引出底下的定義。
|
定義. 數列
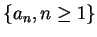 稱為一柯西數列 (Cauchy sequence),
若其滿足下述 稱為一柯西數列 (Cauchy sequence),
若其滿足下述
柯西條件 (Cauchy condition):
|
上定理通常是用來對一事先不知道極限值為何的數列, 證明其收歛。由上二定理知, 一數列收歛, 若且唯若此數列為柯西數列。此稱為柯西收歛判別法
(Cauchy's convergence criterion)。
例 1.設數列
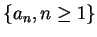 滿足 滿足
證明
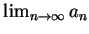 存在。 存在。
例 2.分別求下述三極限值。

(i)
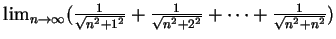 , ,
(ii)
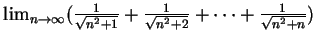 , ,
(iii)
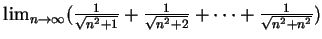 . .
a
進一步閱讀資料:黃文璋(2002).
數列及級數。微積分講義第七章,國立高雄大學應用數學系。
  
|