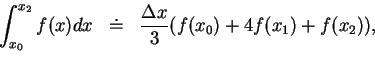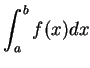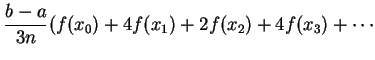定積分之數值計算
若不知 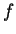 之反導數, 則便無法利用微積分基本定理求定積分
之反導數, 則便無法利用微積分基本定理求定積分
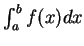 之值。不過我們卻可求此定積分之近似值至其任意精確度。
方法之一便是利用第二章定理
4.9, 以 Riemann 和來逼近。
之值。不過我們卻可求此定積分之近似值至其任意精確度。
方法之一便是利用第二章定理
4.9, 以 Riemann 和來逼近。
在實際應用時, 可取 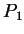 ,
, 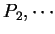 為
為 ![$[a, b]$](img4.gif) 之一正規分割數列若
之一正規分割數列若
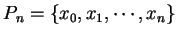 ,
則可以
,
則可以
或
當做第 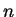 個 Riemann 和, 其中
個 Riemann 和, 其中
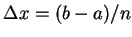 只要
只要 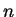 夠大, 可以
夠大, 可以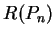 與
與 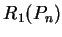 之算術平均 來估計
之算術平均 來估計
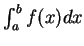 , 通常此為一更好的估計。而
, 通常此為一更好的估計。而
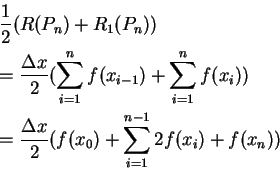
。
因此若
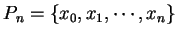 為
為 ![$[a, b]$](img4.gif) 之一正規分割, 則
之一正規分割, 則
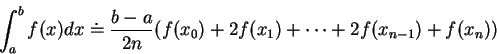 。 。 |
(4.1) |
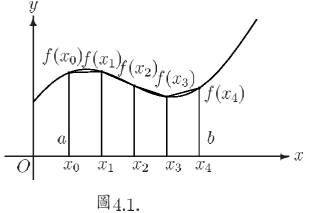
上述積分公式便稱為梯形法
(trapezoidal rule)此名稱之由來如下
設 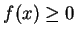 ,
, ![$x\in [a, b]$](img27.gif) , 則如圖 4.1 可看出, (4.1)
式之右側為
, 則如圖 4.1 可看出, (4.1)
式之右側為 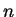 個高皆為
個高皆為
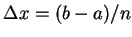 之梯形的面積和
之梯形的面積和
例 1.設
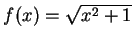 利用梯形法求在
利用梯形法求在 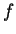 之圖形下,
由 0 至 3 之面積。
之圖形下,
由 0 至 3 之面積。
其次來看梯形法之一推廣, 此法源自於 Simpson (1710-1761),
故稱之為 Simpson 法 (Simpson's rule),
為一較梯形法更精確的估計定積分的方法。
設 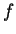 為一在
為一在 ![$[a, b]$](img4.gif) 上連續之函數, 梯形法是以一線段來逼近
上連續之函數, 梯形法是以一線段來逼近 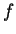 之圖形, 而 Simpson 法是以一拋物線來逼近
之圖形, 而 Simpson 法是以一拋物線來逼近 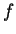 之圖形, 所以又稱拋物線法 (parabolic rule)。我們 先看拋物線的一些性質
給三個不共線之相異點
之圖形, 所以又稱拋物線法 (parabolic rule)。我們 先看拋物線的一些性質
給三個不共線之相異點
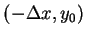 ,
, 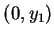 及
及
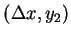 , 恰有一拋物線
, 恰有一拋物線
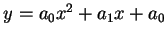
通過此三點, 其中係數 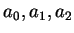 滿足下述三方程式。
滿足下述三方程式。
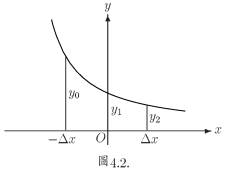
而在此拋物線下, 由 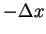 至 之面積 (見圖 4.2) 為
至 之面積 (見圖 4.2) 為
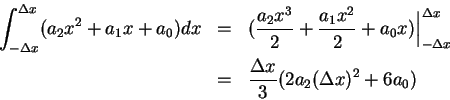
。
由 (4.2)-(4.4), 可證明
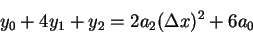
。
此即圖 4.2 中拋物線下的面積。
若將拋物線平移, 設有一拋物線
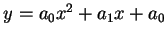 通過
通過 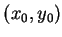 ,
, 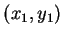 及
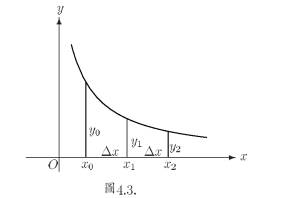
及 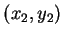 等三點, 見圖 4.3, 其中
等三點, 見圖 4.3, 其中
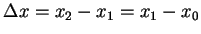 則顯然拋物線下的面積仍相同, 即
則顯然拋物線下的面積仍相同, 即
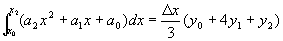 。
。
設
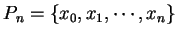 為
為 ![$[a, b]$](img4.gif) 之一正規分割, 其中
之一正規分割, 其中
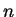 為一偶數, 且令
為一偶數, 且令
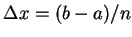 。則
。則
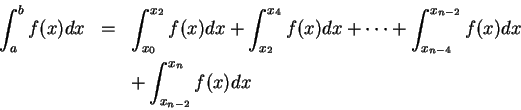
。
其中每一積分
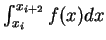 皆可以一通過三點
皆可以一通過三點 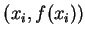 ,
,
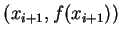 及
及
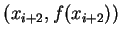 之拋物線下的面積來逼近又由前面已得的結果知:
之拋物線下的面積來逼近又由前面已得的結果知:
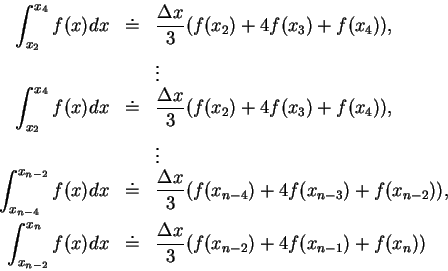
。
將這些式子左、右各分別相加, 即得
即 Simpson 法對積分之逼近。
例 2.試利用 Simpson 法估計
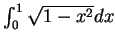 , 取
, 取 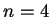 。
。
例 3.求 之圖形上, 由 (1, 1) 至 (5, 1/5) 之弧長的
近似值。
進一步閱讀資料:黃文璋(2002).
積分之應用
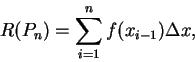
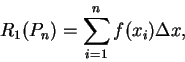
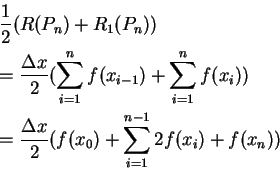 。
。
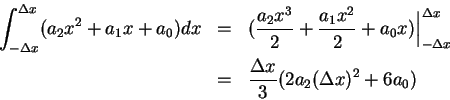 。
。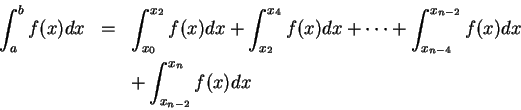 。
。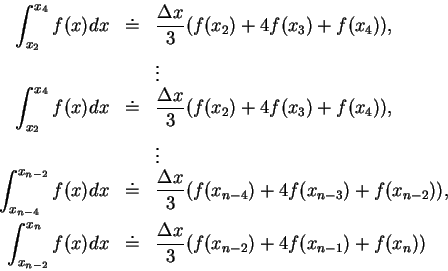 。
。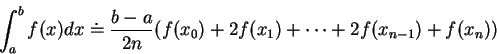 。
。