


弧長及旋轉面積
對平面上一曲線, 欲求其圖形上介於某兩點間之曲線長度,
並稱之為弧長 (arc
length)。為了簡化符號, 以 以P(x)表曲線上一點(x,,f(x))。而若 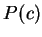 及
及 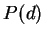 為曲線上二相異點, 以
為曲線上二相異點, 以
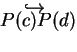 表此二點間之弧 (arc)。即
表此二點間之弧 (arc)。即
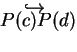 表在曲線上, 由點
表在曲線上, 由點 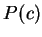 走至
走至 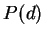 所行經之部分。
所行經之部分。
設 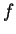 為一定義在閉區間
為一定義在閉區間 ![$[a, b]$](img16.gif) 上的函數, 一個估計
上的函數, 一個估計
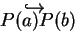 之弧長的方法, 為以內接折線長 之和來估計設
之弧長的方法, 為以內接折線長 之和來估計設
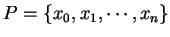 表
表 ![$[a, b]$](img16.gif) 之一分割, 以
之一分割, 以 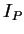 表
表 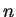 個 線段所組成之折線
個 線段所組成之折線
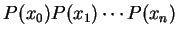
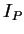 之長度以
之長度以 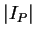 表之, 顯然
表之, 顯然
其中
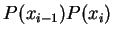 表連接
表連接 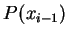 與
與 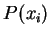 之線段長
之線段長
利用距離公式, 又得
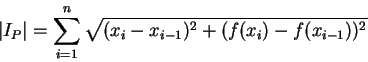 。 。 |
(3.1) |
如果 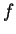 為一可微函數, 則均值定理適用。 因此在
為一可微函數, 則均值定理適用。 因此在
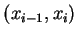 中存在一點
中存在一點 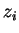 , 使得
, 使得
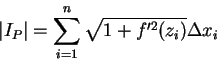
,
其中
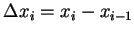 。
。
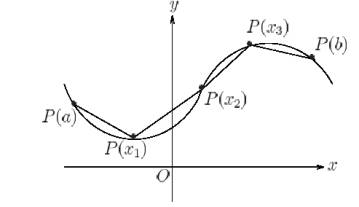
圖 3.1.
若分割的愈來愈細, 我們預期 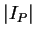 與前述弧長很接近即若
與前述弧長很接近即若
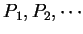 為一數列
為一數列 ![$[a, b]$](img16.gif) 之分割, 滿足
之分割, 滿足
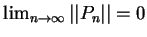 , 則一個合理的猜測是以
, 則一個合理的猜測是以
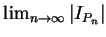 當做
當做
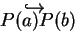 之弧長,
只要此極限存在。 我們給下述定義
之弧長,
只要此極限存在。 我們給下述定義
例 1.求在函數 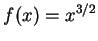 之圖形上,
由
之圖形上,
由 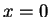 至
至  之弧長。
之弧長。
例 2.求拋物線 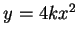 ,
, 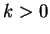 , 介於
, 介於 ![$x\in [a, b]$](img46.gif) 之弧長。
之弧長。
對於不是函數圖形的曲線,
我們常以參數法 (parameter method)
來描述。即以
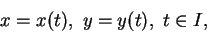 |
(3.5) |
來表示此曲線, 其中 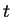 稱為參數。通常假設
稱為參數。通常假設 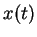 與
與 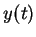 皆為連續函數, 且有相同的定義域。當然以前的函數圖形亦可以
皆為連續函數, 且有相同的定義域。當然以前的函數圖形亦可以
,
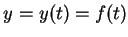
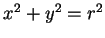 , 其圖形並非一函數圖形,
, 其圖形並非一函數圖形,
為以參數法之表示。 若 ![$I=[a, b]$](img63.gif) , 且
, 且 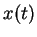 與
與 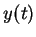 皆為連續可微, 則
(3.5) 描述的曲線之弧長定義為
皆為連續可微, 則
(3.5) 描述的曲線之弧長定義為
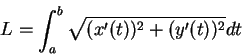 。 。 |
(3.6) |
以 (3.6) 來定義曲線之弧長為定義 3.1
之一推廣。
例 3.求圓 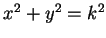 ,
, 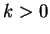 , 之周長。
, 之周長。
例 4.試證橢圓
其中 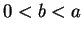 , 之周長為下述積分
, 之周長為下述積分
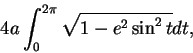 |
(3.7) |
其中
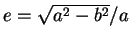 。
。 
最後, 以參數法來求弧長, 也可輕易地推廣至 3 維空間 (甚至 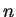 維空間)。
維空間)。
在 6.1
節我們所求都是有關平面上圖形的面積。至於曲面的面積如何求呢? 譬如說一半徑為 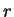 之球的表面積為何?
設有一連續函數
之球的表面積為何?
設有一連續函數 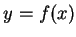 ,
, ![$x\in [a, b]$](img46.gif) , 將
, 將 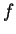 之圖形對
之圖形對 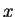 軸旋轉, 得到一旋轉曲面在適當的條件下, 此旋轉曲面的面積是可以求出的。我們先看如何求圓錐側面積。
軸旋轉, 得到一旋轉曲面在適當的條件下, 此旋轉曲面的面積是可以求出的。我們先看如何求圓錐側面積。
例 5.設有一正圓錐, 作二平行底之平面, 將圓錐截出二半徑
分別為 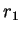 及
及 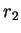 之圓斜面寬設為
之圓斜面寬設為 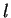 (見圖 3.2)。
則截出之斜面面積 為
(見圖 3.2)。
則截出之斜面面積 為
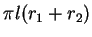 。
。 


例 6.設 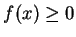 ,
,
![$\forall x\in [a, b]$](img89.gif) , 為一連續可微的函數將
, 為一連續可微的函數將 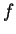 之圖形繞
之圖形繞 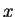 軸旋轉, 以
軸旋轉, 以 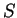 表所得之旋轉面。求
表所得之旋轉面。求 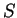 之面積
之面積 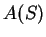 。
。
令
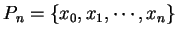 為
為 ![$[a, b]$](img16.gif) 之一分割, 以
之一分割, 以
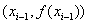 與
與

之連線段,
繞 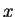 軸旋轉, 得到一如上例中 之圓錐的截面之面積, 當做
軸旋轉, 得到一如上例中 之圓錐的截面之面積, 當做 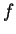 在
在
![$[x_i, x_{i-1}]$](img95.gif) 之圖形繞
之圖形繞 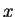 軸旋轉所得旋轉面之面積的近似值。則
軸旋轉所得旋轉面之面積的近似值。則
|
 。 。
|
(3.8) |

再由均值定理知, 存在一
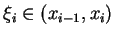 , 使得
, 使得
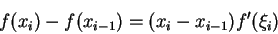
。
得
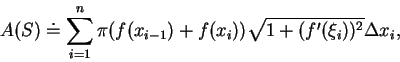 |
(3.9) |
其中
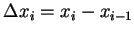 。令
。令  表一數列
表一數列 ![$[a, b]$](img16.gif) 之分割滿足
之分割滿足
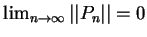 , (3.9)
式之右側其實不是一 Riemann 和, 不過可以證明 (在此略去, 不過參考
(2.5) 式之推導過程不難得到) 當
, (3.9)
式之右側其實不是一 Riemann 和, 不過可以證明 (在此略去, 不過參考
(2.5) 式之推導過程不難得到) 當 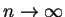 時, 它趨近至
時, 它趨近至
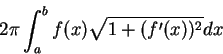
。
我們便定義
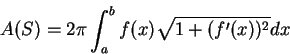 。 。 |
(3.10) |
若 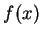 不一定恆為非負, 則
不一定恆為非負, 則
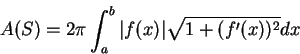 。 。 |
(3.11) |
例 7.求 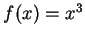 ,
, ![$x\in [0, 2]$](img108.gif) , 之圖形繞
, 之圖形繞 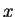 軸旋轉, 所得旋轉面
軸旋轉, 所得旋轉面 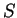 之面積。
之面積。
例 8.求半徑為 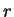 之球的表面積。
之球的表面積。
進一步閱讀資料:黃文璋(2002).
積分之應用
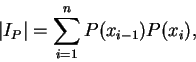
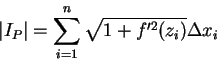 ,
,
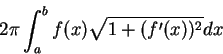 。
。
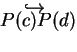 表此二點間之弧 (arc)。即
表此二點間之弧 (arc)。即
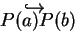 之弧長的方法, 為以內接折線長 之和來估計設
之弧長的方法, 為以內接折線長 之和來估計設
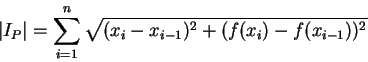 。
。
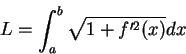 。
。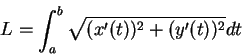 。
。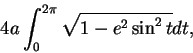



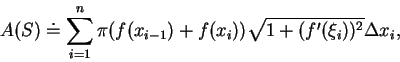
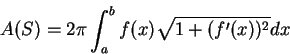 。
。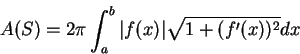 。
。