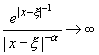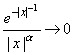函數的其他性質

a

        本單元我們對函數的大小給某種方式的比較，並討論一些特殊而有趣的函數。

  a

（A）函數大小之比較

        比較二函數當其變數很大時，其函數值的大小在微積分中是很重要的，這就是所謂大小的位階。

        對，當，則皆趨近至。但它們趨近至的速度卻不相同。例如，因時，，故趨近至的速度快過。我們便稱比有較高的位階趨近至。同理只要，則比有較高的位階趨近至。

        一般而言，若時，，，且，則稱 趨近至的位階高於。反之，若，當，則稱趨近至的位階低於。而若時，趨近至一不為 0 之常數，或一直介於兩固定正數間，則稱此二函數有相同的位階趨近至。

        例如，設，，則與有相同的位階趨近至，而比有較高的位階趨近至。

        設有二函數及，且趨近至的位階大於，則與有相同的位階。

  a

（B）指數及對數的位階

        在『指數及對數函數之進一步討論』中，我們曾得對 ，

及 。

當時，對同一，愈大便愈大；反之愈小便愈小。但成長的速度慢於任一，而成長的速度快過任一。指數與對數代表兩個極端，將所有的乘冪夾在其間。

        由以上討論知，指數函數趨近至的位階高於任一的乘冪，而對數函數趨近至 的位階低於任一的乘冪。由此又可得到很多位階高於指數函數，或位階低於指數函數的函數。譬如，的位階高於指數函數，而的位階低於指數函數。

        只要夠大，函數x、log x、log(log x)) 、log(log(log x)))等遲早都可大到任意大，但速度卻一個比一個慢。例如，若，這是一個很大的數，但約為 230，而約只為 5.4。

        我們描述一函數趨近至的速度，有時可以說以的某次方，如以的次方趨近至，其中。此表當時，其中為一不等於 0 之常數。也就是前面所說的與有相同的位階。但以指數的速度趨近至，就是位階高於任一，亦即不存在一，使以的次方趨近至 。另一方面，若 的位階高於而低於，則是否存在一，使得的位階與相同，亦即是以的的次方趨近至？答案是否定的。例如，，則時，

， ，

故的位階高於而低於。 但並不存在一，使得，不趨近至 0 或。

        另外，兩函數也不一定可比較其位階之高低。例如，令，其中

，

，    

則時， 且 。但若對每一整數 ，

，                                  

。

故時，之極限既不為 0 也不為 ，又也不會一直介於兩固定正數間。因此無法比較與位階之高低。

        雖然我們對位階的定義並不足以比較任二函數，不過這不是一大缺失。因對諸如上述的及，我們通常不關心其位階的大小，因即使知道其一之值，對另一函數並不能提供有用的資訊。

  a

（C）在任一點的位階

        設對某一，當時，且。則我們也可比較其位階之大小。只要將前面時之位階的比較，稍加修正即可。

        例如，因時，

， ， 。

且

，

故時，趨近至的位階高於，。同理時，因

，

故時， 趨近至 0 的位階低於 ，。

  a

（D）趨近至 0 之位階

         除了比較趨近至的速度，也可比較趨近至 0 的速度。

         例如，因時

， ， ，

且

，

故時， 趨近至 0 的位階高於任意一的乘冪。同理時，因 ，且

，

故時， 趨近至 0 的位階低於任一的乘冪。

  a

（E）記號及記號
         在『泰勒展開式』，我們曾引進記號，對任二函數及， 即表之位階低於，也就是。此記號可適用許多不同的情況。包含函數趨近至 0 或，及參數趨近至或任一 。符號 是源自位階。我們列出一些現有的結果如下。

，

，

，

，            

。           

        另外，我們尚有記號。 表之位階最多與相同。對 ，

，

若且唯若存在一常數，及之一去心鄰域(若，則，其中為某實數)，使得

。

我們讀做is big of at 。例如

，        

，   

，

。      

更一般地，在之符號中，也可不須假設趨近至任一，只要與之比值為有界即可。例如，

，

。

利用記號，有時可更精確地描述誤差。例如，

，

可改為

。

或有

。

又也可以數列取代。例如

。

  a

（F）一些特殊的函數

        底下我們藉幾個形式簡單的函數，讓大家稍微了解有時會有一些我們預期不到的現象發生。

(1) 函數 。     

a

(2)  函數 。          

a

(3)   函數 。     

a

(4)  函數 。     

a

(5)  函數 ， 。     

  a

進一步閱讀資料：黃文璋(2002).  函數的其他性質。微積分講義第五章，國立高雄大學應用數學系。