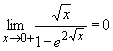指數及對數函數之進一步討論

a

        我們先看指數及對數函數的泰勒展式。

        首先由

，

兩側對 積分，由 0 至 ，得

，

即

。

其中第 次泰勒多項式

，

餘項

。

  a

  a
        下述定理對計算對數的值幫助很大。

  a

  a

例 1.試求 之近似值。    
  a

例 2.試求 之近似值。    
  a

        若利用 記號，由以上的結果可得

，

。              

  a

例 3.試證

。    

  a

        底下我們來看比 ，更一般的結果。 

  a

  a
        利用此定理，立即可得

又仿上述定理，亦可得一關於連續變數的結果。

  a

  a
例 4.假設以打字機打字，且設每個字會打錯的機率為 ， 。以 表打個字後總共錯的字數，則為何？    
  a

        對數函數及指數之漸增或漸減，有許多有趣的性質，底下為一例。

  a
例 5.設

試證 為一增函數。     
  a

       在『對數』中，我們曾提過對數函數成長緩慢。相反地，指數函數成長極快速。下述定理顯示，對數函數成長速度較任意正的乘冪皆慢，而指數函數之成長快過任意之乘冪。

  a

  a

        利用記號，上定理可表示為

不論 多大及 多小，只要二者皆為正，則 趨近至 的速度慢過 ，而 趨近至的速度又慢過 。

  a

例 6.求 。      

  a

        在『極限之不定形』我們曾提過尚有一些不定形之極限未處裡，即 和 的形式，這些經適當地轉換後，皆可化為 或 的不定形。有關對數或指數的不定形，也常可藉助前定理來處理。

  a

例 7.試證 。      

  a

例 8.求 。      

  a