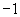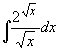指數函數

  a

          為一嚴格單調漸增之函數，且滿足，。故對，恰存在一，使得。即為一由映至之且映成的函數。因此之反函數存在，我們以表之。函數之定義域為，值域為，且仍為連續及嚴格漸增。
       欲知之值為何，我們需先找到對數值為之，則。又因對數函數為函數，且其值域為，故，恰有一解。

        現對每一有理數，因

，，

，

得

，

故

。

即對每一有理數，之值為的次方。若，其中為二整數且 ，則的定義為。
        若為無理數，一個最自然的定義值的辦法是令

，

又因為一連續函數，故對任一有理數列，只要，則

。

即為之極限。此後對任一實數，我們便將寫成。而， ，便稱為指數函數，此為一定義在實數上之嚴格漸增且連續的函數，並取正值。另外，也將寫成。

  a

        對於

，

可有一較一般的形式，即將表示為下述極限

。    

此為另一求的步驟。

  a

        其次我們來看任意一正數的次方如何定義，到目前為止我們只知有理次方的意義明確。

        設且為一有理數，則

。

上式又可改寫為

。

而此式右側對每一實數皆有定義，因此對及，我們以上式來定義：

，，。（1）

由此定義也立即看出對，，，為一連續函數，且對任一正數 ，及任一實數，有意義了。
        由（1）式即得

，，。（2）

令，即，則（1）式成為

， 。

更一般的結果為，

，， 。（3）

另外，亦有乘積公式：

利用指數及對數可求出一些我們以前算不出的積分及微分。

  a

例 1. 在第三章『微積分基本定理』中，我們已能對每一不為之有理數，得到

。

至於，上一單元已討論過，便是導致對數。為無理數時，若能求出定積分

，

則便可得在任一不包含 0 之區間上之定積分。     

  a

例 2. 在第二章『導數的定義及基本性質』中，我們曾得到對任一有理數，

。

在此我們想將上述公式推廣至任意實數。     
  a

        由上二例知，對任一實數，

。

但

只對才成立。對，只要，微分會使次方少 1，積分會使次方多 1。此因時，，而 1 的微分為 0，並非。故不會是的某一次方，也沒有任一的次方之微分為。幸好有將此情況補起來， ，而 。

  a

  a

        上定理指出，

。（5）

這是指數函數最特殊的一個性質，即它的導數仍為它本身。

  a

        其次我們來看一般以任意一正數為底的指數函數。

        我們已定義，，也定義了，，。至於底不是的指數函數，也不難定義。

        比照（1）式，令

， ，。

我們列出其指數的性質：

  (1) ，

  (2) ，

  (3) ，

  (4) ，

  (5) ，若且唯若 ，其中 。
  a

  a

        由（5）式及（6）式，利用微積分基本定理，即得下述積分公式。

        利用變數代換，上二式又導致更一般的關於指數的積分公式。即對每一連續可微的函數 ，

  a

例 3. 分別求 及 之導數。    

  a
        對於上例，有幾件須特別留意的。首先設有二可微的函數 及 ，及二常數，為實數。則

，

。

但 並不屬於上兩類函數之一，而是有 的形式，即底與指數皆為函數。

        另外， 的運算程序如何？事實上

，

也就是指數部分由上往下算。一般而言

。

上式右側其實等於 ，與並不相同。當 時，上式左側為 ，右側為 ，二者不等。至於 或 2 時，上式左、右相等。

  a

例 4. 求 。    
  a

例 5. 求 。    

  a

例 6. 求 。    

  a

例 7. 求 。    

  a

        最後我們來看指數函數之圖形。

  a
例 8. 試繪 ，，之圖形。    

  a

例 9. 試繪 ，，之圖形。    
  a

進一步閱讀資料：黃文璋(2002).  指數函數。微積分講義第五章，國立高雄大學應用數學系。