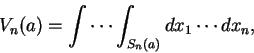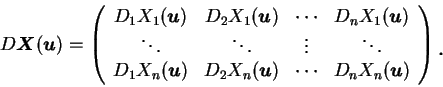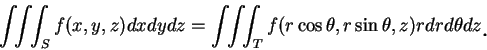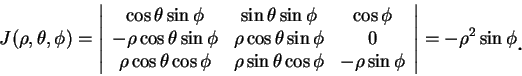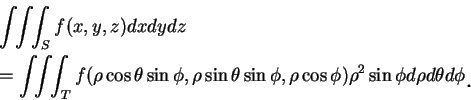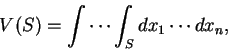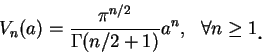高
維 重 積 分
a 重積分的概念可由二維空間推廣至 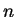 維空間, 其中
維空間, 其中 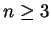 。由於其架構完全類似二維的情況, 所以我們只描述主要的結果。
。由於其架構完全類似二維的情況, 所以我們只描述主要的結果。
如 10.1 節所述, 假設有一定義在 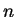 維空間之純量函數
維空間之純量函數 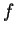 , 則
, 則 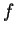 在
在
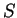 之積分, 稱為
之積分, 稱為 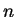 重積分, 且以
重積分, 且以
表之。當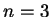 , 我們以
, 我們以 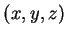 取代
取代
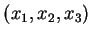 , 且以
表三重積分。
, 且以
表三重積分。 仿定義二重積分的方式, 我們仍可藉助階梯函數, 定義函數 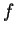 之
之 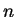 重積分。而
重積分。而 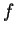 為可積的條件也類似二重積分所需的條件, 可參考定理
3.2. 在適當的條件下,
為可積的條件也類似二重積分所需的條件, 可參考定理
3.2. 在適當的條件下, 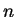 重積分也可經由
重積分也可經由 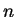 次逐次積分求出積分值。
次逐次積分求出積分值。
二重積分裡的變數代換公式, 也可立即推廣至 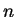 重積分。設
重積分。設
令
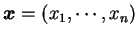 ,
,
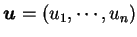 ,
,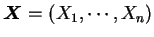 , 則上述這些等式定義出一由
, 則上述這些等式定義出一由 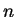 維空間中之一集合
維空間中之一集合 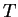 映至另一
映至另一 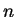 維空間之集合
維空間之集合 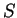 的向量值函數
我們假設函數
的向量值函數
我們假設函數 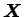 為
為
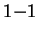 且在
且在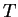 中連續可微。則
中連續可微。則 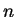 維的積分變換公式為
維的積分變換公式為
|

|
(6.1) |
其中
 |
(6.2) |
而
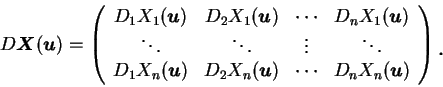
如同在二維的情況, 代換公式 (6.1) 當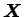 為在
為在 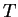 中之
中之 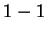 變換, 且 Jacobian
變換, 且 Jacobian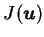 在
在 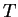 中皆不為 0 成立。當然若在
中皆不為 0 成立。當然若在
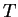 中一“體積” (在
中一“體積” (在 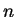 維空間中我們以體積的稱呼取代面積) 為
0的積分中,
維空間中我們以體積的稱呼取代面積) 為
0的積分中,
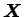 不為
不為
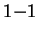 或在這種集合中
或在這種集合中
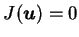 , 則代換公式仍成立。
, 則代換公式仍成立。
當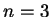 , 我們以
, 我們以 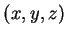 取代
取代
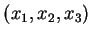 , 以
, 以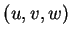 取代
取代
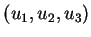 , 以
, 以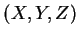 取代
取代
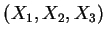 , 則三重積分之代換公式成為
, 則三重積分之代換公式成為

其中
底下我們來看兩個三維裡重要的變換。
例6.1.圓柱座標 (cylindrical coordinates)。以  取代
取代
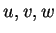 , 且令
, 且令
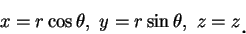
即以  之極座標代換
之極座標代換  及
及 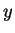 , 而
, 而 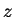 不變。欲使此代換為
不變。欲使此代換為
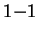 ,
, 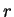 須為正, 而
須為正, 而
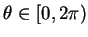 。圖 6.1 顯示一在
。圖 6.1 顯示一在 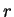 -
-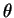 -
-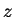 空間中的長方體映至
空間中的長方體映至
 -
-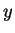 -
-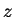 空間中的形狀。
空間中的形狀。

圖 6.1. 圓柱座標之轉換
對圓柱座標, Jacobian 為
故代換公式為
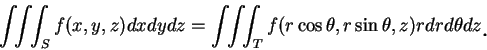
當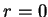 時, Jacobian
時, Jacobian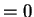 , 但因這種點的集合在三度空間中之體積為
0, 故不影響 代換公式的有效性。
, 但因這種點的集合在三度空間中之體積為
0, 故不影響 代換公式的有效性。
例 2.球座標 (spherical coordinates)。我們以
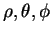 取代
取代
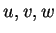 , 且令
, 且令
圖 6.2 顯示此代換的幾何意義。

圖 6.2. 球座標之轉換
欲使此代換為
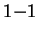 , 取
, 取 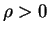 ,
,
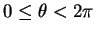 ,
,
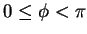 。對任意常數
。對任意常數  ,
曲面
,
曲面 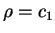 , 表以一原點為球心, 半徑為
, 表以一原點為球心, 半徑為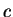 之 球面; 曲面
之 球面; 曲面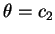 , 為一通過
, 為一通過 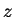 軸之平面; 而曲面
軸之平面; 而曲面 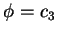 , 表一以
, 表一以 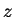 為中心軸之正圓錐。故一
為中心軸之正圓錐。故一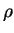 -
-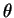 -
-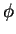 空間中之長方體, 在
空間中之長方體, 在
 -
-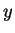 -
-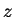 空間中的形狀 如圖 6.2 所示。
空間中的形狀 如圖 6.2 所示。
這種代換之 Jacobian 為
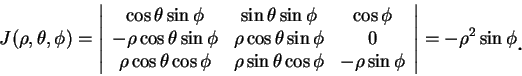
因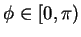 ,
,
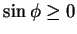 , 故
, 故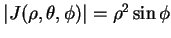 , 且代換公式成為
, 且代換公式成為
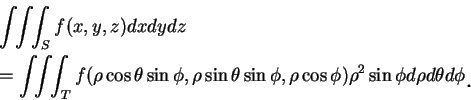
再度地, 雖當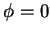 時
時
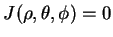 , 但因在三維空間中,
, 但因在三維空間中,
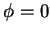 之點的集合之體積為 0, 故代換公式仍有效。
之點的集合之體積為 0, 故代換公式仍有效。
利用重積分也可求一 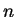 維立體的體積。設有一
維立體的體積。設有一 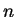 維的集合
維的集合 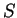 ,
則
,
則 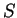 之體積為
之體積為
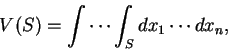
當然欲上式成立, 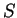 也須有些限制才行。
也須有些限制才行。
例 3.求在拋物面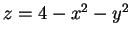 之下, 且在平面
之下, 且在平面 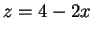 之上的立體的體積。
之上的立體的體積。 
例 4.令 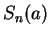 表一
表一 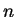 維半徑
維半徑 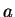 的實心球, 即令
的實心球, 即令
且令
表 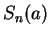 之體積。則
之體積。則
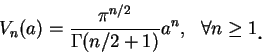 |
(6.3) |

進一步閱讀資料:黃文璋(2002).
高維重積分。微積分講義第十章,國立高雄大學應用數學系。