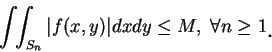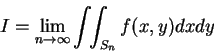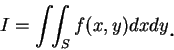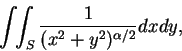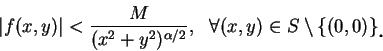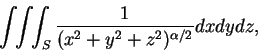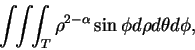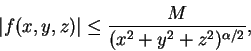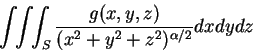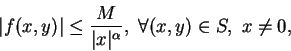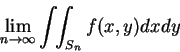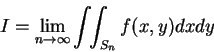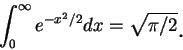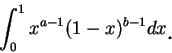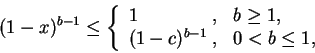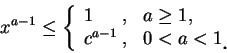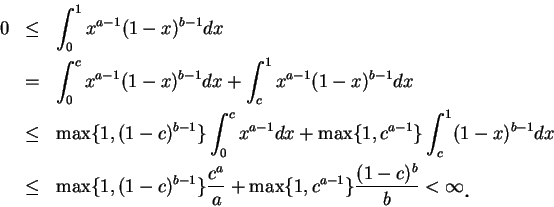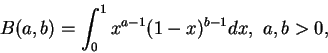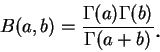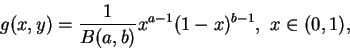10.7瑕重積分

瑕重積分

　　如同單變數的情況, 我們須將重積分擴展到所謂瑕積分。我們主要仍有兩種瑕積分, 其一為函數不為有界, 其二為積分區域不為有界。

　　我們先看第一種瑕積分。在大多數我們擬求的積分, 其積分算子可能在積分區域中連續, 或只在一些隔離的點或沿著某一曲線不連續。但不論那一種情況, 這些例外的點之面積須為零。我們可以一小區域 s 包含這些例外的點, 求在 $S\setminus s$ 之積分, 然後當 s 之面積趨近至 0 時, 求在 $S\setminus s$ 之積分的極限。若此極限存在, 則將此極限值定義為在上的瑕積分。由於我們希望此極限與趨近至的方式無關, 因此我們將做一較強的限制, 即要求不僅是 , 且 $\vert f\vert$ 之瑕積分存在 (相當於在級數裡要求絕對收斂, 而非條件收斂)。我們先敘述下定理。

定理 1.設積分區域為有界且之面積存在。又設存在一數列之單調漸增且封閉的之子區域 $\{S_n, n\geq 1\}$ , 即 $S_1\subset S_2\subset\cdots\subset S_n\subset\cdots\subset S$ , 使得在每一皆有定義且連續。又設之面積趨近至之面積 , 即

$\begin{displaymath} \lim_{n\rightarrow \infty } A(S_n)=A(S), \end{displaymath}$

(7.1)

且設存在一 , 使得

$\begin{displaymath} \int\!\!\int_{S_n}\vert f(x, y)\vert dxdy\leq M,\ \forall n\geq 1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(7.2)

(即 $\vert f\vert$ 在 , $n\geq1$ , 的積分為均勻有界)。則

$\begin{displaymath} I=\lim_{n\rightarrow \infty }\int\!\!\int_{S_n} f(x, y)dxdy \end{displaymath}$

(7.3)

存在, 且與 $\{S_n\}$ 之選取無關。　　　　　　　　　　　　　　

　　我們便以上定理中之用來定義在上之瑕積分, 即

$\begin{displaymath} I=\int\!\!\int_S f(x, y)dxdy\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(7.4)

在證明定理 1 之前, 我們看一些例子, 以說明此定理之想法。

例 1.考慮函數

$\begin{displaymath} f(x, y)=\log\sqrt {x^2+y^2}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

則在區域 $S=\{(x, y)\vert x^2+y^2\leq 1\}$ 之積分為何？　　

例 2.考慮積分

$\begin{displaymath} \int\!\!\int_{S} \frac 1{(x^2+y^2)^{\alpha /2}}dxdy, \end{displaymath}$

(7.5)

其中 , 。此積分收斂若且唯若 $\alpha <2$ 。　　

　　由上述結果我們可得到一判別二重瑕積分收斂之充分條件 (但絕非必要條件) 如下:

設函數在有界區域除了可能在某一點外, 此點為了簡便取為 (0,0), 皆連續。又設存在一及一常數 $\alpha <2$ , 使得

$\begin{displaymath} \vert f(x, y)\vert<\frac M{(x^2+y^2)^{\alpha /2}},\ \ \foral... ... y)\in S\setminus \{(0,0)\}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(7.6)

則 $\int\!\!\int_S f(x, y)dxdy$ 收斂。

a　　
例 3.我們可將上例的結果推廣到三維的情況。考慮三重積分

$\begin{displaymath} \int\!\!\int\!\!\int_S\frac 1{(x^2+y^2+z^2)^{\alpha /2}}dxdydz, \end{displaymath}$

其中有界區域包含原點, 利用球座標之轉換, 原積分成為

$\begin{displaymath} \int\!\!\int\!\!\int_T\rho^{2-\alpha }\sin\phi d\rho d\theta d\phi, \end{displaymath}$

其中為對應之 $(\rho,\theta ,\phi)$ 之範圍。仿上例之討論可得若 $\alpha <3$ 則原積分收斂。

　　同樣地, 設除了在 (0,0,0) 外, 在有界區域上連。又設存在一及一常數 $\alpha <3$ 使得

$\begin{displaymath} \vert f(x,y,z)\vert\leq \frac {M}{(x^2+y^2+z^2)^{\alpha /2}}, \end{displaymath}$

則 $\int\!\!\int\!\!\int_S f(x,y,z)dxdydz$ 收斂。

　　更一般地, 設為一有界區域, 在上連續, 則若 $\alpha <3$ ,

$\begin{displaymath} \int\!\!\int\!\!\int_S\frac {g(x,y,z)}{(x^2+y^2+z^2)^{\alpha /2}}dxdydz \end{displaymath}$

收斂。

　　若積分算子在某一曲線上皆為無限大 (或負無限大), 則瑕積分也有可能存在。最簡單的情況為, 積分算子在一直線中的一部分, 譬如說軸, 為無限大。此時若

$\begin{displaymath} \vert f(x, y)\vert\leq \frac {M}{\vert x\vert^{\alpha }},\ \forall (x, y)\in S,\ x\neq 0, \end{displaymath}$

其中 , $\alpha <1$ , 則 $\int\!\!\int_S f(x, y)dxdy$ 存在。若欲證明, 只要先將去掉一包含 $S\cap y$ 軸之長方形, 且令此長方形之面積趨近至 0 即可。

　　其次我們來看積分區域不為有界的第二種瑕積分。再度地, 我們並不想考慮最一般的情況, 而只想對我們實際上最常碰到的情況, 提出一收斂性的判別法。

　　設為一無界的區域, 且函數在上連續。仍以一數列之單調漸增的子集合 $S_1\subset S_2\subset\cdots\subset S$ 來逼近 , 其中每一皆設為封閉且有界。但因不為有界,

$\begin{displaymath} \lim_{n\rightarrow \infty }A(S_n)=A(S) \end{displaymath}$

在此就不一定有意義了。所以我們不假設上式成立, 而要求之每一封閉且有界的子集, 必須至少包含在其一中。例如, 若為整個 - 平面, 則可取成以 (0,0)為圓心且半徑為之圓。若

$\begin{displaymath} \lim_{n\rightarrow \infty }\int\!\!\int_{S_n}f(x,y)dxdy \end{displaymath}$

存在, 且與 $\{S_n, n\geq 1\}$ 之選取無關, 則此極限值便定義為在上的積分, 且以 $\int\!\!\int_S f(x, y)dxdy$ 表之。我們有底下的判別定理, 其證明因類似定理 1 故略去。

定理 2.設積分區域不為有界。若存在一數列之單調漸增且封閉的之子區域 $\{S_n, n\geq 1\}$ , 使得之每一封閉且為有界的子集, 必包含在某一中, 且設存在一 , 使得

$\begin{displaymath} \int\!\!\int_{S_n}\vert f(x, y)\vert dxdy\leq M,\ \forall n\geq 1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

則

$\begin{displaymath} I=\lim_{n\to\infty }\int\!\!\int_{S_n}f(x,y)dxdy \end{displaymath}$

存在, 且與 $\{S_n\}$ 之選取無關。

　　我們便以上定理中之作為在上之瑕積分。

在第七章例 5.7 我們曾給一瑕積分中的重要結果, 即

$\begin{displaymath} \int_0^{\infty }e^{-x^2/2}dx=\sqrt {\pi/2}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(7.11)

由變數代換知, (7.11) 等價於

(7.12)

底下我們來看如何經由重積分得到 (7.12)。

例 4.試證 (7.12)成立。

　　因此經由二重積分, 我們可得到此一分析中重要的瑕積分的值。由於 $e^{-x^2}$ 之不定積分並非初等函數, 故若欲直接求此定積分值是很困難的。

　　附帶一提, 定理 1 及定理 2 之求二重積分的瑕積分, 其步驟都是很合乎直覺的。此二定理如何得到(7.13)?

　　其次考慮下述積分:

$\begin{displaymath} \int_0^1 x^{a-1}(1-x)^{b-1}dx\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

當 , 此為一正常積分, 但當或 , 則此為一瑕積分。底下我們來看, 事實上只要 , 則此瑕積分收斂。

　　對任一 , $0<x\leq c$ 時,

$\begin{displaymath} (1-x)^{b-1}\leq \left\{\begin{array}{lll} 1 &\hspace{-0.25cm... ... (1-c)^{b-1}&\hspace{-0.25cm}, & 0<b\leq 1, \end{array}\right. \end{displaymath}$

而時,

$\begin{displaymath} x^{a-1}\leq \left\{\begin{array}{lll} 1 &\hspace{-0.25cm}, &... ...& 0<a< 1\mbox{\raisebox{-1.2mm}{\large . }} \end{array}\right. \end{displaymath}$

故

$\begin{eqnarray*} 0 &\leq& \int_0^1 x^{a-1}(1-x)^{b-1}dx \\ &=&\int_0^c x^{a-1}... ...-1}\}\frac {(1-c)^b}b<\infty \mbox{\raisebox{-1.2mm}{\large . }} \end{eqnarray*}$

我們便定義函數為

$\begin{displaymath} B(a, b)=\int_0^1 x^{a-1}(1-x)^{b-1}dx, \ a, b>0, \end{displaymath}$

且稱之為 beta 函數。如同, 也需藉助重積分才能求出 , 見下例。

例 5.試證

$\begin{displaymath} B(a, b)=\frac {\Gamma(a)\Gamma(b)}{\Gamma(a+b)}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}$

(7.14)

　　由上述討論立即得到一重要的機率密度函數, 即

$\begin{displaymath} g(x,y)=\frac 1{B(a, b)}x^{a-1}(1-x)^{b-1},\ x\in(0,1), \end{displaymath}$

(7.18)

其中為二常數。

例 6.求 , 其中 , $2\ell-k>1$ , 。

　　在第七章例 5.11, 我們曾討論一些 Dirichlet 積分之斂散性, 那時也指出 $\int_0^{\infty }\sin x/xdx=\pi/2$ 。底下我們看利用重積分, 將可輕易地求出此積分值。

例 7.試證 (i) $\int_0^{\infty }\sin x/xdx=\pi/2$ ; (ii) $\int_0^{\infty }(1-\cos x)/x^2 dx=\pi/2$ 。

進一步閱讀資料：黃文璋(2002). 瑕重積分。微積分講義第十章，國立高雄大學應用數學系。