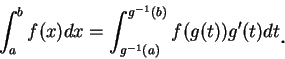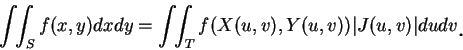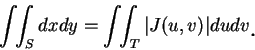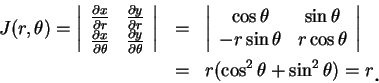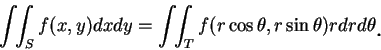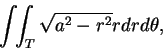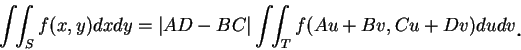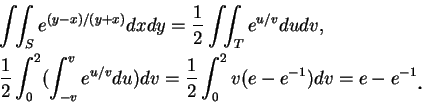變 數 代 換
a
在單變函數的積分中, 變數代換為一重要的積分技巧, 許多複雜的積分,
往往可藉助變數代換, 而轉成較簡單的形式因而積出。此法是基於下述公式:
|
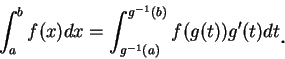
|
(5.1)
|
在第 3.3 節, 於 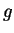 為連續可微及
為連續可微及 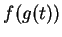 為連續的條件下,
我們證明上式成立。
為連續的條件下,
我們證明上式成立。
對於兩個變數, 我們也有一類似 (5.1) 的公式,
也就是二重積分的變數代換公式, 此公式可將一在  -
-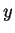 平面上一區域
平面上一區域 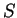 上的積分
上的積分
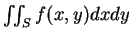 , 轉為一在
, 轉為一在
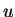 -
-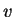 平面上一區域
平面上一區域 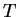 的二重積分
的二重積分
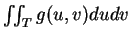 。底下我們便將給出
。底下我們便將給出 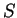 與
與 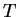 的關係及
的關係及 與
與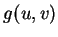 的關係。
的關係。
二重積分的變數代換, 較一維的情況複雜許多。此因有二變數要代換,
亦即不若在 (5.1) 中只有一函數 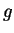 出現, 現在會有二函數, 以
出現, 現在會有二函數, 以 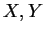 表之, 此二函數結合
表之, 此二函數結合 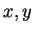 與
與 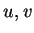 如下:
如下:
|
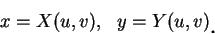
|
(5.2)
|
上述二函數將 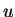 -
-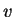 平面上一點
平面上一點 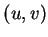 映至
映至 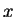 -
-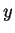 平面上一點
平面上一點
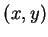 。而
。而 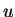 -
-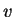 平面上一集合
平面上一集合 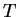 便映至
便映至 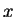 -
-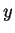 平面上一集合
平面上一集合 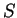 。
。
有時由 (5.2) 中之二式, 可解出 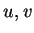 以
以 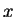 及
及 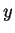 表之, 即得
表之, 即得
上述二式定義出一由 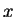 -
-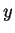 平面至
平面至 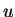 -
-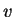 平面的映射, 稱為 (5.2)
所定義之映射的反映射。1
平面的映射, 稱為 (5.2)
所定義之映射的反映射。1 1 映射為一特例, 即
1 映射為一特例, 即 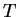 中不同的點映至
中不同的點映至 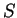 中不同的點。
中不同的點。
我們將只考慮 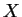 及
及 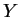 為連續函數, 且
為連續函數, 且
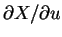 ,
,
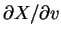 ,
,  ,
,
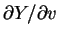 , 等偏導數皆為連續。對
, 等偏導數皆為連續。對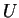 及
及 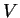 也做類似的假設。大部分我們實際遇到的函數, 皆會滿足這些條件。
二重積分的變數代換公式為
也做類似的假設。大部分我們實際遇到的函數, 皆會滿足這些條件。
二重積分的變數代換公式為
|
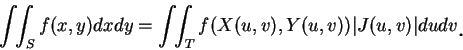
|
(5.3)
|
上式右側積分算子中的 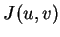 , 與 1 維公式中的
, 與 1 維公式中的 所扮演的角色相同。此項稱 Jacobian determinant (行列式), 或只稱
Jacobian, 它等於
所扮演的角色相同。此項稱 Jacobian determinant (行列式), 或只稱
Jacobian, 它等於
有時以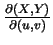 取代
取代 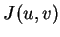 。
。
(5.3) 式的證明可參考 Apostol (1974) Theorem 15.11。 除了前述關於
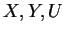 及
及 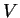 之假設外, 尚須設由
之假設外, 尚須設由 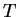 至
至 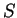 之映射為 1
之映射為 1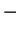 1 且
1 且
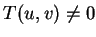 。不過若只是在一面積為 0 的集合中, 此映射不為
1
。不過若只是在一面積為 0 的集合中, 此映射不為
1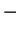 1 或 Jacobian 為 0, 則 (5.3) 式仍成立。當
1 或 Jacobian 為 0, 則 (5.3) 式仍成立。當 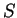 為一 矩形且
為一 矩形且
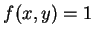 ,
,
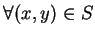 , 則 (5.2) 式成為
, 則 (5.2) 式成為
|
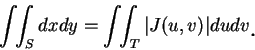
|
(5.4)
|
即使對此特例, 證明也不容易。藉助 Green 定理, Apostol (1969)
Section 11.29 給了 一 (5.4) 式之證明。然後在 Section 11.30,
由此特例導出 (5.3) 式。
Jacobian 可視為二維變數代換過程中, 由 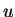 -
-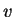 平面至
平面至 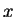 -
-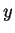 平面, 一邊長分別
平面, 一邊長分別 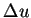 及
及 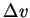 的矩形的面積變化因子。關於這方面的幾何解釋, 可參考 Apostol (1969) pp.394-396。
的矩形的面積變化因子。關於這方面的幾何解釋, 可參考 Apostol (1969) pp.394-396。
我們來看一些例子。
例 1.極座標 (polar coordinates)。令
則此為在 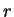 -
-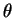 平面上矩形
平面上矩形
![$[0,a]\times [0, 2\pi)$](img46.gif) 之任一子集上的
之任一子集上的
 變換。此變換之 Jacobian 為
變換。此變換之 Jacobian 為
故轉換公式成為
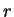 -
-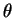 平面上一矩形對應至
平面上一矩形對應至 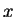 -
-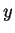 平面上一扇形, 如圖 5.1。當
平面上一扇形, 如圖 5.1。當
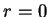 時 Jacobian 為 0, 但因
時 Jacobian 為 0, 但因 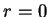 之點的集合之面積為 0,
故不影響轉換公式的成立。
之點的集合之面積為 0,
故不影響轉換公式的成立。
若積分區域的邊界是沿著 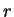 或
或 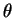 為常數,
則極座標的轉換便會很適合。例如, 在求第一卦限之半徑為
為常數,
則極座標的轉換便會很適合。例如, 在求第一卦限之半徑為 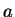 之球的體積, 即求
之球的體積, 即求
其中
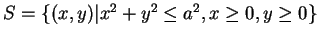 。若變換為極座標, 積分成為
。若變換為極座標, 積分成為
其中 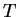 為矩形
為矩形
![$[0,a]\times [0,\pi/2)$](img56.gif) 。上述積分可很容易地求出為
。上述積分可很容易地求出為 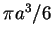 。
。
例 2.線性變換 (linear transformations)。考慮下述線性變換:
|
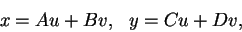
|
(5.5)
|
其中 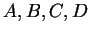 為常數。則 Jacobian 為
為常數。則 Jacobian 為
為了使 Jacobian 不為 0, 我們假設 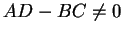 , 如此才能由 (5.5)
解出
, 如此才能由 (5.5)
解出 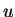 及
及 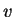 。
。
原來平行的二直線, 經過線性變換, 仍為平行。故 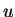 -
-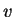 平面上一矩形, 經此變換後, 成為
平面上一矩形, 經此變換後, 成為 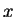 -
-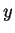 平面上一平行四邊形,
而面積為原來矩形的面積乘上
平面上一平行四邊形,
而面積為原來矩形的面積乘上 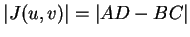 。變換公式為
。變換公式為
舉一個例子來看, 考慮積分
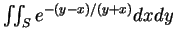 ,
其中
,
其中 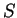 為由直線
為由直線 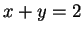 及二座標軸所構成之三角形, 見圖 5.2。由於積分算子中有
及二座標軸所構成之三角形, 見圖 5.2。由於積分算子中有 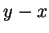 及
及 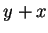 , 所以令
, 所以令
解出 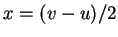 ,
, 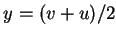 ,
, 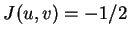 。欲求在
。欲求在  -
- 平面上
平面上 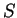 之映象, 因直線
之映象, 因直線 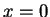 及
及 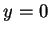 分別映至直線
分別映至直線  及
及
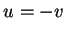 , 且直線
, 且直線 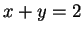 映至
映至  。故
。故  為一三角形,
為一三角形,  ,
,
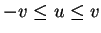 。因此
。因此
a
進一步閱讀資料:黃文璋(2002).
變數代換。微積分講義第十章,國立高雄大學應用數學系。