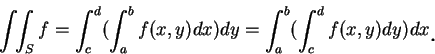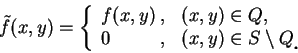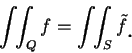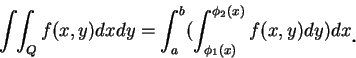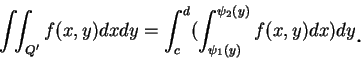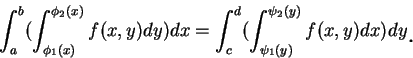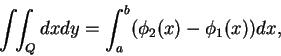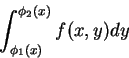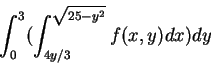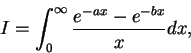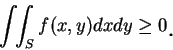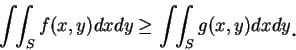重積分之進一步討論

  a

　　在第二章定理 4.7, 對單一變數, 利用閉區間上的連續函數必為均勻連續的性質, 我們證明閉區間上的連續函數為可積。對兩個變數的函數, 我們亦有類似的結果, 證明在此略去, 可參考 Apostol (1969) Theorem 11.6。

定理 1.設 $f$ 在矩形 $S=[a,b]\times [c,d]$ 連續, 則 $f$ 在 $S$ 上可積, 且

\begin{displaymath} \int\!\!\int_S f=\int_c^d(\int_a^b f(x,y)dx)dy=\int_a^b(\int_c^d f(x,y)dy)dx\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(3.1)

　

　　第二章系理 4.2 指出, 只在有限個點不連續的一個閉區間上的有界函數, 仍為可積。對一閉矩形上的兩個變數的有界函數, 只要其不連續的點 “不太多”, 此函數仍有可能可積。我們先給下述定義。

　

定義 1.設$A$ 為平面上一有界的集合, 若 , 存在有限個矩形,其聯集包含 $A$, 且矩形總面積小於$\vspace*{0.1cm}$, 則稱 $A$ 之面積為 0。

由上定義知, 下述各集合之面積均為 0:

(i) 平面上有限個點之集合;

(ii) 平面上有限個面積為 0 之集合之聯集;

(iii) 一面積為 0 之集合的任一子集;

(iv) 任一線段。

　

定理 2.設 $f$ 為一在矩形 $S=[a,b]\times [c,d]$ 上之有界函數, 且其不連續點的面積為 0, 則 $f$ 在 $S$ 上之二重積分存在。

　

　　至此為止, 我們討論的二重積分, 都是在一矩形上。我們可將積分範圍推廣到更一 般的區域。

　　設 $Q$ 為一平面上有界的區域, 且設 $Q$ 包含於一矩形 $S$ 中。設 $f$ 為一定義在 $Q$ 之有界函數。定義一新函數 $\tilde {f}$ 在 $S$ 如下:

\begin{displaymath} \tilde {f}(x, y)=\left\{\begin{array}{lll} f(x, y) &\hspace{... ...tminus Q\mbox{\raisebox{-1.2mm}{\large . }} \end{array}\right. \end{displaymath}

(3.2)

即將 $f$ 之定義域擴展至 $S$, 而將在 $Q$ 之外的函數值令為 0。現在的問題是, 這樣定義出來的函數 $\tilde {f}$ 是否在 $S$ 中可積? 若是的話, 我們便稱 $f$ 在 $Q$ 可積, 且定義

\begin{displaymath} \int\!\!\int_Q f=\int\!\!\int_S\tilde {f}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

　　首先我們考慮下述 $x$-$y$ 平面上的區域:

\begin{displaymath} Q=\{(x, y)\vert a\leq x\leq b, \phi_1(x)\leq y\leq \phi_2(x)\}, \end{displaymath}

其中 $\phi_1$ 及 $\phi_2$ 為閉區間 $[a, b]$ 上之連續函數, 且 $\phi_1(x)\leq \phi_2(x)$, $\forall x\in [a, b]$。 為了易於區分, 我們稱此為第一 型之區域, 圖 3.1 為一例。因 $\phi_1$ 及 $\phi_2$ 皆在 $[a, b]$ 連續, 故為有界, 因此這種區域為有界。垂直線 $x=t$ 與 $Q$ 之交集為一線段, 由 $y=\phi_1(x)$ 至 $y=\phi_2(x)$。


圖 3.1. 第一型的區域        　　　　            圖 3.2. 第二型的區域

　　另一類我們擬考慮的 $x$-$y$ 平面上的區域為:

\begin{displaymath} Q'=\{(x, y)\vert c\leq y\leq d,\ \psi_1(y)\leq x\leq \psi_2(y)\}, \end{displaymath}

其中 及為 $[c, d]$ 上之連續函數, 且, $\forall y\in [c, d]$。我們稱此為第二型之區域, 圖 3.2 為一例。此時一水平線與 $Q'$ 之交集為一線段。易見這種區域亦為有界。

　　我們所考慮的區域, 將是第一型或第二型, 或可以分成有限個第一型或第二型的區域。

　　現設 $f$ 為一定義在一第一型的區域 $Q$ 之有界函數。以一矩形 $S$ 來包含 $Q$, 並定義函數 $\tilde {f}$ 如 (3.2)。$\tilde {f}$ 在 $S$ 中之不連續點, 包含 $f$ 在 $Q$ 中之 不連續點與在 $Q$ 之邊界上且 $f$ 之值不為 0 之點。而 $Q$ 之邊界為如圖 3.1 的 $\phi_1$ 與 $\phi_2$ 之圖形與二垂直線段所組成。此二線段的面積為 0, 而此二圖形之面積亦為 0 。

　　下定理指出, 若 $f$ 在 $Q$ 之內點 (以 int$Q$ 表之) 連續, 則二重積分 $\int\!\!\int_Q f$ 存在。 在此

\begin{displaymath} \mbox{int\,} Q=\{(x, y)\vert a<x<b,\ \phi_1(x)<y<\phi_2(x)\}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

　

定理 3.設 $Q$ 為一第一型的區域, 介於函數 $\phi_1$ 與 $\phi_2$ 的圖形間, $x\in [a, b]$。又設 $f$ 為一定義在 $Q$ 之有界函數, 且在 int$Q$ 連續。則二重積分 $\int\!\!\int_Q f$ 存在, 且其值可由二次逐次積分求得, 即

\begin{displaymath} \int\!\!\int_Q f(x, y)dxdy=\int_a^b(\int_{\phi_1(x)}^{\phi_2(x)}f(x, y)dy)dx\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(3.3)證明

　

　　當然, 我們亦有一對應第二型區域的結果。即若 $f$ 為一定義在第二型區域 $Q'$ 之有界函數, 且在 int$Q'$ 連續, 則 $f$ 在 $Q'$ 可積, 且

\begin{displaymath} \int\!\!\int_{Q'}f(x, y)dxdy=\int_c^d(\int_{\psi_1(y)}^{\psi_2(y)}f(x, y)dx)dy\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(3.5)

　　又有些區域同時為第一型及第二型, 如一圓盤 (即圓及其內部的區域), 此時積分順序便不重要, 且

\begin{displaymath} \int_a^b(\int_{\phi_1(x)}^{\phi_2(x)}f(x, y)dy)dx =\int_c^d(... ...y)}^{\psi_2(y)}f(x, y)dx)dy\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

在某些情況下, 此二種積分之一可能會比另一計算上容易許多, 此由底下的一些例子中可看出。在積分前最好略微評估一下何者較易計算。

　　設 $Q=\{(x, y)\vert a\leq x\leq b, \phi_1(x)\leq y\leq \phi_2(x)\}$ 為一 第一型的區域。取 $f(x, y)=1$, $\forall (x,y)\in Q$, 則由定理 3 知

\begin{displaymath} \int\!\!\int_Q dxdy =\int_a^b(\phi_2(x)-\phi_1(x))dx, \end{displaymath}

而由一維的積分結果知, 上式右側等於區域 $Q$ 之面積, 故知利用二重積分可求面積。

　　另外, 若 $f$ 為一定義在 $Q$ 之非負且連續的函數, 則積分

\begin{displaymath} \int_{\phi_1(x)}^{\phi_2(x)}f(x, y)dy \end{displaymath}

表一平行 $y$-$z$ 平面對 $f$ 在 $Q$ 上之縱集所截出之平面的面積, 見圖 3.3 中之陰影部分。(3.3) 式即指出 $f$ 在 $Q$ 中之二重積分等於此截面面積的積分。故二重積分 $\int\!\!\int_Q f$ 等於 $f$ 在 $Q$ 上之縱集的體積。 一般而言, 若 $f$ 與 $g$ 皆在 $Q$ 連續, 且 $f\leq g$, 則二重積分 $\int\!\!\int_Q(g-f)$ 等於介於二函數 $f$ 與 $g$ 之圖形間的立體的體積。 對一第二型的區域也可有類似的解釋。

圖 3.3.

　　底下我們給一些例子。


例 1.令 $f(x, y)=(2y-1)/(x+1)$, $S$ 為由三直線 $x=0$, $y=0$ 及 $2x-y-4=0$ 所圍出之區域。求 $f$ 在 $S$ 上之二重積分。   提示

\begin{picture}(0,80)(-100,80)\thicklines\put(0,115){\vector(1,0){110}} \put(50,... ...\put(80,105){$2$} \put(33,52){$-4$} \put(80,115){\line(-1,-2){30}} \end{picture}



圖 3.4.

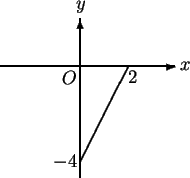
例 2.求介於二拋物線 $y=x^2$ 與 $y=4-x^2$ 間之區域 $Q$ 的 面積, 見圖 3.5。  提示

圖 3.5.


例 3.求在曲面 $z=4-x^2-4y^2$ 之下, 而在 $x$-$y$ 平面一區域 $Q$ 之上的立體 $W$ 的體積, 其中 $Q$ 為 $x=0$, $y=0$ 及 $x+2y-2=0$ 所圍出之區域, 見 圖 3.6。  提示

圖 3.6.



例 4.求在平面 $z=x+2y$ 之下, 與四分之一圓柱 $x^2+y^2\leq 4$, $x$, $y\geq 0$, $z\geq 0$, 間之立體的體積。  提示


例 5.求下述橢球所圍出之體積:    提示

\begin{displaymath} \frac {x^2}{a^2} + \frac {y^2}{b^2}+\frac {z^2}{c^2}=1\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}    

例 6.試將 $\int_0^1\int_{x^2}^x f(x, y)dydx$ 交換積分順序, 假設此交換為合法。  提示

例 7.試將

\begin{displaymath} \int_0^3(\int_{4y/3}^{\sqrt {25-y^2}}f(x, y)dx)dy \end{displaymath}

交換積分順序, 假設此交換為合法。   提示

　

　　定理 1 的交換連續函數的積分順序, 有許多不同的應用。例如, 有一些單變函數的定積分, 若該函數的不定積分無明確的形式 (即非初等函數), 有時可藉由此定理求出積分值。

例 8.求 $\int_0^1 (x^2-1)/\log xdx$。   提示

例 9.求下述積分值

\begin{displaymath} I=\int_0^{\infty }\frac {e^{-ax}-e^{-bx}}{x}dx, \end{displaymath}

其中 $a, b>0$。   提示

　

　　關於重積分, 尚有一些與一維中類似的結果, 我們只列出一些, 證明也都類似一維中的證明, 因此皆略去。

(i) 設 , $\forall (x, y)\in S$, 則

\begin{displaymath} \int\!\!\int_S f(x, y)dxdy\geq 0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(ii) 設 , $\forall (x, y)\in S$, 則

\begin{displaymath} \int\!\!\int_S f(x, y)dxdy\geq \int\!\!\int_S g(x, y)dxdy\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(iii) $\vert\int\!\!\int_S f(x, y)dxdy\vert\leq \int\!\!\int_S \vert f(x, y)\vert dxdy$。

　　        

進一步閱讀資料：黃文璋(2002). 重積分之進一步討論。微積分講義第十章，國立高雄大學應用數學系。