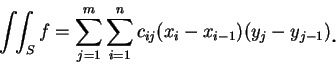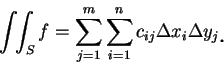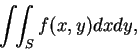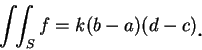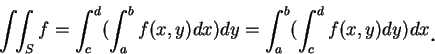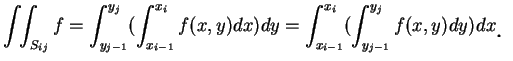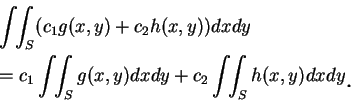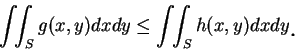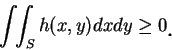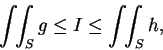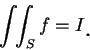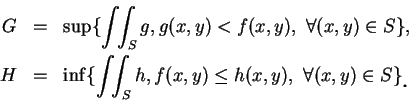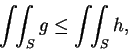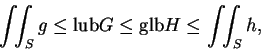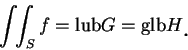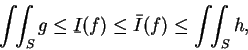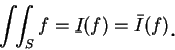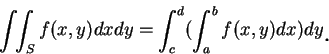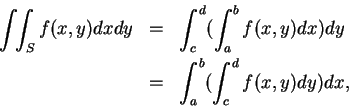二重積分之定義 a
設  為平面上一矩形, 且為
為平面上一矩形, 且為 ![$[a, b]$](img3.gif) 及
及 ![$[c, d]$](img4.gif) 之笛卡兒乘積, 即
之笛卡兒乘積, 即
又設 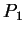 及
及 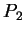 分別為
分別為 ![$[a, b]$](img3.gif) 及
及 ![$[c, d]$](img4.gif) 之分割, 其中
之分割, 其中
笛卡兒乘積 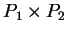 便稱為
便稱為  之一分割, 且將
之一分割, 且將  分割成
分割成
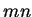 個子矩形 。
個子矩形 。  之一分割
之一分割 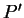 若滿足
若滿足 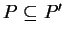 , 便稱為
, 便稱為 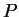 之一細分。設
之一細分。設  為一定義在
為一定義在
 上之函數, 若存在
上之函數, 若存在  之一分割
之一分割 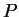 , 使得
, 使得  在每一開的子矩形上為常數, 便稱
在每一開的子矩形上為常數, 便稱  為一階梯函數。此處一不包含邊界之矩形便稱開的矩形。一階梯函數在其每一子矩形之邊界的值,
在積分中並不重要。易見若
為一階梯函數。此處一不包含邊界之矩形便稱開的矩形。一階梯函數在其每一子矩形之邊界的值,
在積分中並不重要。易見若  及
及 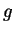 為
為  上之二階梯函數,
則其線性組合
上之二階梯函數,
則其線性組合 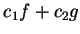 仍為一階梯函數。
仍為一階梯函數。
現設
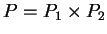 為
為  之一分割, 其中
之一分割, 其中
 ,
,
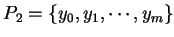 , 而
, 而
 為一在
為一在  上之階梯函數, 即
上之階梯函數, 即  在前述分割中之每一子矩形為常數。以
在前述分割中之每一子矩形為常數。以 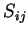 表
表
![$[x_{i-1},x_i]\times
[y_{j-1}, y_j]$](img21.gif) , 且設
, 且設  在
在 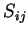 之內點取值
之內點取值 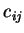 。若
。若 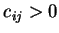 , 則以
, 則以 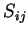 為底,
為底, 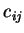 為高之長方體之體積為
為高之長方體之體積為
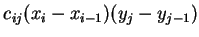 。現將所有前述乘積加起來,
便定義為
。現將所有前述乘積加起來,
便定義為  在
在  上 之二重積分。即
上 之二重積分。即
|
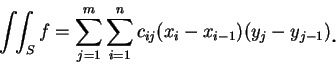
|
(2.1)
|
如同在單變數的情況, 若以 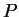 之一細分
之一細分 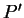 取代
取代 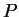 ,
則積分值不變, 亦即積分值與分割無關, 只要
,
則積分值不變, 亦即積分值與分割無關, 只要  在每一開的子矩形為常數。
在每一開的子矩形為常數。
令
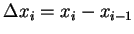 ,
,
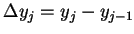 ,
, 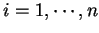 ,
,
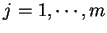 , 則 (2.1) 成為
, 則 (2.1) 成為
|
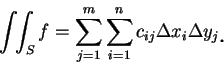
|
(2.2)
|
上式左側有時也寫成
這樣寫的好處是易於與 (2.2) 右側對照, 提醒我們此和之由來。
若  在
在  之內點皆為常數, 譬如說
之內點皆為常數, 譬如說
則
|
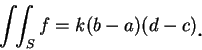
|
(2.3)
|
又因
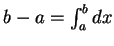 ,
,
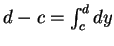 , 故 (2.3) 式可改寫為
, 故 (2.3) 式可改寫為
|
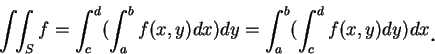
|
(2.4)
|
也就是對一常數函數, 我們可以二次逐次積分, 來求 一二重積分。此二者本質上是不同的, 二次逐次積分乃是在做兩次單變函數的積分。稍後大家會看到, 雖有時計算也是有些不易,
但每一次我們只是在做一單變函數的積分,
其過程內涵上較重積分簡單多了。各位可試以第二章引進單變函數的積分的方式, 先定義下和及上和,
然後定義下積分及上積分, 而當二者相等, 便稱  在
在  可積, 其共同值即為
可積, 其共同值即為  在
在  之二重積分的值。底下我們稍改變一下方式,
這也是許多教科書引進單變函數積分的方式, 不過原理其實是一樣的。我們先定義階梯函數之積分, 然後再定義較一般的函數之積分。但仍如單變數的情況, 此定義並無法有效地求積分值。幸好我們遇到的重積分, 大都可化為逐次積分。
之二重積分的值。底下我們稍改變一下方式,
這也是許多教科書引進單變函數積分的方式, 不過原理其實是一樣的。我們先定義階梯函數之積分, 然後再定義較一般的函數之積分。但仍如單變數的情況, 此定義並無法有效地求積分值。幸好我們遇到的重積分, 大都可化為逐次積分。
對一階梯函數  ,
,
|
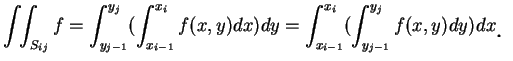
|
(2.5)
|
底下這些關於階梯函數的性質, 都可由 (2.2) 式或利用 (2.5) 證出。定理中之函數  及
及  皆為定義在矩形
皆為定義在矩形  上之階梯函數, 又
上之階梯函數, 又  為一非退化之 矩形, 即
為一非退化之 矩形, 即  不為一點或一線段。
不為一點或一線段。
|
定理 1.(線性). 對任二常數  及 及 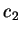 , ,
|
a
a
其次我們定義一在一矩形上為有界之函數的二重積分。設  為一在矩形
為一在矩形  上 之有界函數, 即設
上 之有界函數, 即設
則  介於二階梯函數
介於二階梯函數 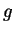 與
與 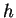 之間, 其中
之間, 其中 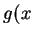 ,
, 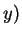
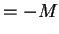 ,
,
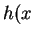 ,
, 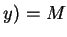 ,
, 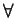
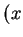 ,
, 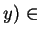
 。若存在唯一之實數
。若存在唯一之實數 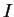 , 使得
, 使得
|
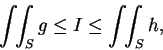
|
(2.6)
|
對所有滿足
|
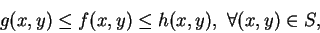
|
(2.7)
|
之階梯函數 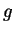 、
、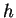 成立, 則稱
成立, 則稱  在
在  上可積, 且積分值為
上可積, 且積分值為
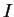 , 即
, 即
底下提到的 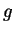 及
及 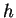 仍皆為階梯函數。令
仍皆為階梯函數。令
因  為一有界函數, 故
為一有界函數, 故 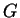 及
及 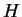 皆非空集合。又因
皆非空集合。又因
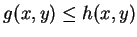 ,
,
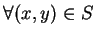 , 故
, 故
因此 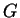 中每一元素皆小於或等於
中每一元素皆小於或等於 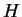 中任一元素。 即知
中任一元素。 即知 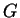 有最小上界, 而
有最小上界, 而 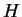 有最大下界, 並滿足
有最大下界, 並滿足
只要 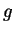 ,
, 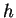 滿足 (2.7) 式。故知
滿足 (2.7) 式。故知 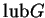 及
及 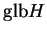 皆滿足 (2.6) 式。結論是,
皆滿足 (2.6) 式。結論是,  在
在  上可積若且唯若
上可積若且唯若
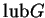
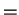
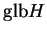 , 且此時
, 且此時
我們以 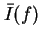 表
表 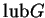 , 並稱為
, 並稱為  在
在  中之下積分, 以
中之下積分, 以
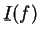 表
表 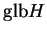 , 並稱之為
, 並稱之為  之
之  中之上積分。由以上的討論便得下述定理。
中之上積分。由以上的討論便得下述定理。
a
我們可看出若要依重積分的定義, 來求積分值, 將是一件艱鉅的工作。底下的定理, 便提供一經由二次逐次積分來求二重積分的值之方法。
在利用 (2.8) 式求二重積分時, 我們先將 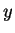 固定, 而將
固定, 而將  對
對 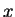 由
由 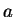 至
至 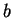 積分, 然後再將所得之一
積分, 然後再將所得之一 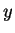 的函數, 對
的函數, 對 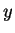 由
由 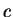 至
至
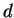 積分。在類似的條件下, 即設
積分。在類似的條件下, 即設
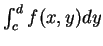 存在,
存在,
![$\forall
x\in [a, b]$](img93.gif) , 且設此積分在
, 且設此積分在 ![$[a, b]$](img3.gif) 可積, 則可將
可積, 則可將  先對
先對 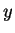 再對
再對 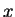 積分, 且
積分, 且
|

|
(2.9)
|
而若二條件皆滿足, 則
即可交換積分順序。讀者也可試將此結果與第九章定理 8.4 比較,
此處交換積分順序 所需條件顯然較弱。
我們也可對定理 5 給一幾何的解釋。若  為非負,
則三維空間中的點
為非負,
則三維空間中的點 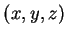 的集合, 其中
的集合, 其中 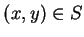 ,
,
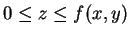 , 稱為
, 稱為  在
在  上之縱集。此集合以
上之縱集。此集合以 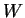 表之,
它包含所有在曲面
表之,
它包含所有在曲面 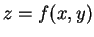 之下, 而在矩形
之下, 而在矩形  之上的所有點。
對
之上的所有點。
對
![$\forall y\in [c, d]$](img79.gif) , 積分
, 積分
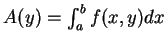 , 為被一 平行
, 為被一 平行
 -
-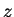 平面之平面, 所截出之截面的面積。又因截面積
平面之平面, 所截出之截面的面積。又因截面積 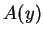 , 在
, 在
![$[c, d]$](img4.gif) 可積, 故由 6.2
節之結果知,
可積, 故由 6.2
節之結果知,
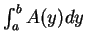 即等於
即等於 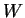 之體積
之體積 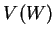 。故當
。故當  為非負時, 定理 5 證明
為非負時, 定理 5 證明  在
在  上之縱集之體積, 即為
上之縱集之體積, 即為  在
在  之重積分。
之重積分。
另外, (2.9) 式則提供另一計算縱集之體積的方式。此次我們先求平行
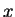 -
-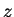 平面之平面所截出 之面積。
平面之平面所截出 之面積。
例 1.令
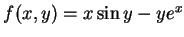 ,
,
![$S=[-1,1]\times[0,\pi/2]$](img106.gif) ,
求
,
求  在
在  之二重積分。
之二重積分。 
例 2.令
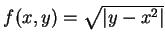 ,
,
![$S=[-1,1]\times [0,2]$](img111.gif) 。求
。求  在
在  之二重積分。
之二重積分。 
例 3.求在
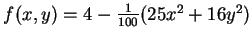 之圖形下, 而在
矩形
之圖形下, 而在
矩形 ![$S=[0, 2]\times [0, 3]$](img125.gif) 之上的立體
之上的立體  之體積。
之體積。 
進一步閱讀資料:黃文璋(2002).
二重積分之定義。微積分講義第十章,國立高雄大學應用數學系。