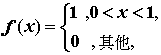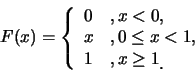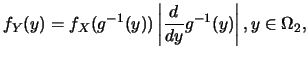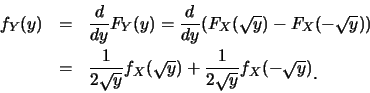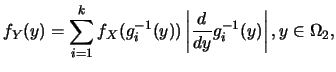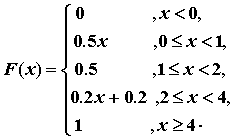|
  
變
數 代 換
對一隨機變數 , 有時我們會想知道它的一個函數 , 有時我們會想知道它的一個函數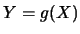 的行為。 的行為。 便稱為 便稱為 之變數代換(change of variable)。 之變數代換(change of variable)。 仍為一隨機變數。通常 仍為一隨機變數。通常 的分佈知道,
而因 的分佈知道,
而因 的值是由 的值是由 的值所決定, 故 的值所決定, 故 的分佈,
可由所給之 的分佈,
可由所給之 的分佈來決定。 的分佈來決定。
對每一實數的子集合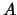 , ,
|
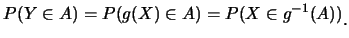
|
(5.1)
|
在此
對於新的隨機變數 , 由(5.1)式, 欲求 , 由(5.1)式, 欲求 落在某一集合 落在某一集合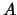 之機率,
仍要回到關於 之機率,
仍要回到關於 的機率。 的機率。
例 1. 設 為一離散型的隨機變數, 且p.d.f.為 為一離散型的隨機變數, 且p.d.f.為

令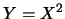 , , 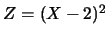 。求 。求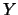 及 及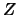 之分佈為何? 之分佈為何? 
例 2. 設隨機變數 之p.d.f.為 之p.d.f.為
令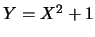 , ,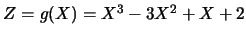 。求 。求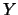 及 及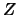 之分佈為何? 之分佈為何? 
例 3. 設隨機變數 有 有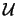 (0,1)分佈。即其p.d.f.為 (0,1)分佈。即其p.d.f.為
分佈函數為
令
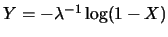 , 其中 , 其中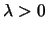 為一常數。 為一常數。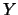 之機率密度函數為何? 之機率密度函數為何? 
例 4. 設隨機變數 之p.d.f.為 之p.d.f.為
令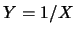 。則此為一由 。則此為一由 至 至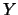 之 之 變換,
且 變換,
且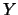 取值在 取值在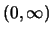 。我們想決定 。我們想決定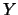 之p.d.f.。 之p.d.f.。 
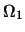 表 表 之機率密度函數取正值處。這種集合稱為分佈之支撐(support)。另外對一函數 之機率密度函數取正值處。這種集合稱為分佈之支撐(support)。另外對一函數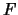 , ,
表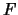 在 在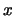 之左極限值。同理可定義右極限 之左極限值。同理可定義右極限 。只是若 。只是若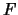 為分佈函數, 因其為右連續, 故 為分佈函數, 因其為右連續, 故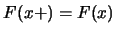 , ,
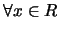 。 。
定理 1適用連續及離離散型的隨機變數。當 之機率密度函數為連續,
則利用定理 1, 可由微分分佈函數而得。 之機率密度函數為連續,
則利用定理 1, 可由微分分佈函數而得。
例 5. 設 有 有
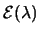 分佈。令 分佈。令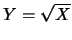 。則 。則
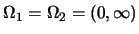 , 且 , 且 之p.d.f. 之p.d.f.
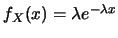 , , 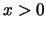 , 在 , 在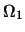 中連續; 中連續;
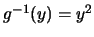 在 在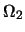 之導數 之導數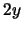 為連續。故 為連續。故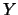 之p.d.f.為 之p.d.f.為
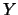 稱為具有參數 稱為具有參數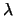 之瑞萊分佈(Rayleigh distribution)。 之瑞萊分佈(Rayleigh distribution)。
例 6. 設隨機變數 有 有
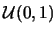 分佈.令 分佈.令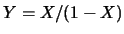 。試決定 。試決定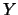 之p.d.f.及分佈函數。 之p.d.f.及分佈函數。 
在做變數代換時, 函數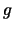 有時不為嚴格單調, 因此定理 2就不適用。
但往往會有 有時不為嚴格單調, 因此定理 2就不適用。
但往往會有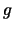 在一個個的集合中, 分別為嚴格單調, 因此在每一個集合中, 皆可解出 在一個個的集合中, 分別為嚴格單調, 因此在每一個集合中, 皆可解出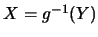 ,
則仍有辦法求出 ,
則仍有辦法求出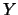 之分佈。 之分佈。
例 7. 設 為一連續型的隨機變數, 令 為一連續型的隨機變數, 令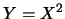 。則對 。則對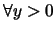 , ,
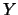 之分佈函數為 之分佈函數為
此處用到 為連續型, 所以 為連續型, 所以
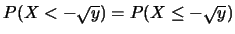 。 。
現若 之p.d.f.存在, 則 之p.d.f.存在, 則
我們發現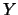 之p.d.f.為兩項之和,
分別對應區間 之p.d.f.為兩項之和,
分別對應區間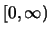 及 及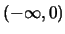 。 。
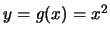 在前者有反函數 在前者有反函數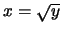 ,
在後者有反函數 ,
在後者有反函數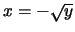 。 。
定理
1推廣如下:
對一分佈函數, 我們定義其分位函數(quantile
function,
有時也稱反函數(inverse
function),
但與一般反函數的定義不同)如下:
若一隨機變數 以 以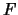 為分佈函數,
則 為分佈函數,
則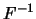 可同時稱為 可同時稱為 及 及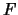 之分位函數。即使 之分位函數。即使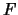 不一定是連續,
也不一定嚴格漸增, 不一定是連續,
也不一定嚴格漸增, 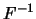 必定存在。但若 必定存在。但若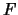 為連續, 且嚴格漸增,
則 為連續, 且嚴格漸增,
則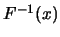 等於滿足 等於滿足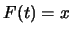 之唯一的 之唯一的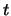 。此時 。此時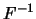 與一般反函數的意義相同。 與一般反函數的意義相同。
對
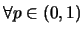 , 令 , 令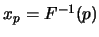 。
則 。
則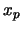 稱為此分佈之第 稱為此分佈之第
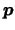 分位數( 分位數(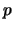 th-quantile), 或第 th-quantile), 或第
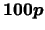 百分位數( 百分位數(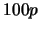 th-percentile)。
特別地 th-percentile)。
特別地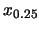 稱為下四分位數(lower quartile), 稱為下四分位數(lower quartile),
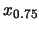 稱為上四分位數(upper quartile)。先給 稱為上四分位數(upper quartile)。先給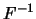 的一些基本性質。 的一些基本性質。
例 8. 設隨機變數 有 有
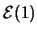 分佈。則 分佈。則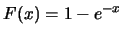 , ,
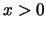 。由於在 。由於在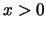 處, 處, 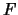 為嚴格漸增,
故 為嚴格漸增,
故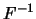 即 即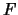 之反函數。經由解 之反函數。經由解
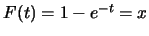 ,
得 ,
得
 。
。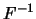 之圖形給在圖5.1。 注意 之圖形給在圖5.1。 注意
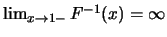 。 。

圖5.1
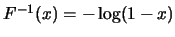 之圖形 之圖形
例 9. 設有分佈函數
則在![$x\in (0,0.5]$](img179.gif) , 解 , 解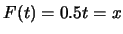 , 得 , 得
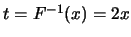 ; 在 ; 在
![$x\in
(0.5,0.6]$](img182.gif) , , 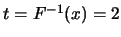 ; 在 ; 在![$x\in (0.6,1]$](img184.gif) ,
解 ,
解
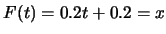 , 得 , 得
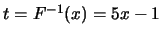 。分位函數通常不定義在 。分位函數通常不定義在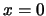 及 及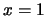 , 不過在本例中, , 不過在本例中,
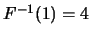 有定義。 有定義。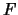 之0.3分位數為0.6, 0.5分位數為1,
0.55分位數為2, 0.6分位數亦為2。 之0.3分位數為0.6, 0.5分位數為1,
0.55分位數為2, 0.6分位數亦為2。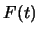 在 在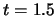 連續, 但 連續, 但
又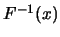 在 在 連續, 但 連續, 但
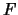 及 及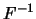 之圖形如圖5.2. 之圖形如圖5.2.
圖 5.2 例 9中 及 及 之圖形 之圖形
給一分佈函數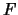 ,
利用其分位函數 ,
利用其分位函數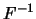 及一有 及一有
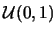 分佈的隨機變數,
可得一以 分佈的隨機變數,
可得一以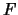 為分佈函數之隨機變數, 此過程即所謂分位轉換(quantile
transformation)。 為分佈函數之隨機變數, 此過程即所謂分位轉換(quantile
transformation)。
當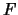 為連續時, 定理 4有下述逆定理。 為連續時, 定理 4有下述逆定理。
例 10. 設隨機變數 之分佈函數為 之分佈函數為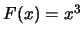 , ,  。令 。令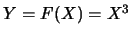 。驗證 。驗證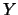 有 有
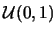 分佈。 分佈。 
例 11. 設隨機變數 有標準的羅吉斯分佈, 即分佈函數 有標準的羅吉斯分佈, 即分佈函數
驗證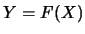 有 有
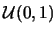 分佈。 分佈。 
進一步閱讀資料:黃文璋 (2003) .
基本概念。數理統計講義第一章。國立高雄大學應用數學系。
  
|
|
|