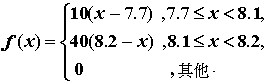|
  
分佈函數與機率密度函數
對一隨機變數 , 其累積分佈函數(cumulative
distribution function, 縮寫為c.d.f.), 通常簡稱為分佈函數,
縮寫為d.f., 又稱分布函數, 或分配函數: , 其累積分佈函數(cumulative
distribution function, 縮寫為c.d.f.), 通常簡稱為分佈函數,
縮寫為d.f., 又稱分布函數, 或分配函數:
|
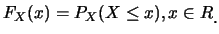
|
(4.1)
|
如果隨機變數 很清楚, 很清楚, 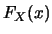 也可只寫成 也可只寫成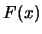 。 。
分佈函數是一定義域為實數, 對應域為區間![$[0,1]$](img6.gif) 的函數。完全不同的機率空間,
是可能得到相同的分佈函數。 的函數。完全不同的機率空間,
是可能得到相同的分佈函數。
例 1. 投擲一公正的銅板3次, 令 表所得之正面數。 則其分佈函數為何? 表所得之正面數。 則其分佈函數為何? 
分佈函數是定義在整個實數上,
而非只定義在 取值的集合
。 取值的集合
。
定理 1. 一函數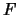 為一分佈函數, 若且唯若下述諸條件成立: 為一分佈函數, 若且唯若下述諸條件成立:
(i)
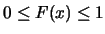 , ,
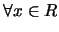 ; ;
(ii) 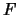 為一非漸減函數; 為一非漸減函數;
(iii) 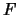 為一右連續函數; 為一右連續函數;
(iv)
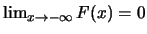 , 且 , 且
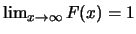 。 。 |
設隨機變數 之分佈函數為 之分佈函數為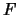 , 則對 , 則對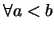 , 因 , 因
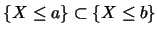 , 故 , 故
即
|
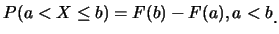
|
(4.3)
|
以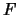 表示出一些與 表示出一些與 有關之常見事件的機率如下: 有關之常見事件的機率如下:
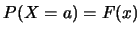 之圖形在 之圖形在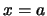 跳升之高度, 跳升之高度,
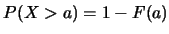 , ,
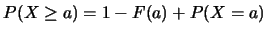 , ,
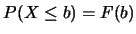 , ,
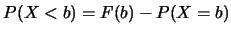 . .
又對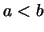 , ,
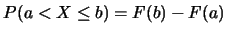 , ,
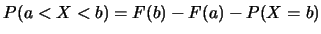 , ,
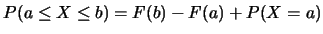 , ,
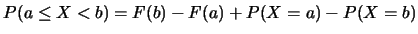 . .
例 2. 投擲一出現正面的機率為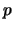 之銅板, 之銅板, 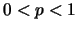 ,
直到出現一正面才停止。令 ,
直到出現一正面才停止。令 表總共之投擲數。則 表總共之投擲數。則
|
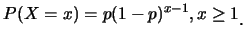
|
(4.4)
|
因此對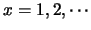 ,則其分佈函數為何? ,則其分佈函數為何? 
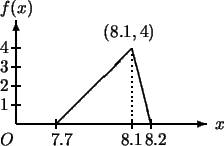
例 3. 設
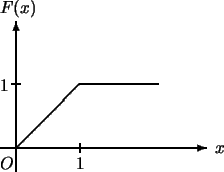
圖4.2給出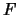 之圖形。 之圖形。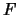 為一連續函數, 滿足定理1中之四個條件,
故為一分佈函數。 為一連續函數, 滿足定理1中之四個條件,
故為一分佈函數。
圖4.2 例 3中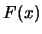 之圖形 之圖形
例 4. 考慮
|
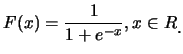
|
(4.5)
|
驗證此函數是否為一分佈函數? 

圖 4.3
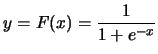 , , 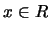 , 之圖形 , 之圖形
隨機變數 之分佈函數 之分佈函數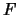 若為連續函數, 便稱 若為連續函數, 便稱 為連續型;
若 為連續型;
若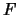 為階梯函數, 便稱 為階梯函數, 便稱 為離散型。也可稱分佈函數為連續型或離散型。不過也有既非離散亦非連續的隨機變數。 為離散型。也可稱分佈函數為連續型或離散型。不過也有既非離散亦非連續的隨機變數。
離散型隨機變數, 其分佈函數的圖形, 有跳升之處的集合, 必為可數的,
可能是一有限集合, 或可數的無限集合。
在同一樣本空間,
可以有不同的隨機變數, 但分佈函數卻相同, 在不同的樣本空間,
亦可分別定義隨機變數, 而有相同的分佈函數。
定義 1. 二隨機變數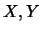 , 若滿足 , 若滿足
|
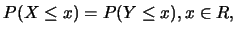
|
(4.6)
|
則稱分佈相同, 並以
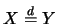 表之。 表之。 |
若以 分別表 分別表 及 及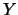 之分佈函數。 之分佈函數。 與 與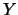 分佈相同,
表 分佈相同,
表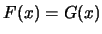 , ,
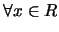 。即 。即 與 與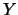 有相同的分佈函數。分佈相同就是分佈函數相同, 也可說有共同的分佈。 有相同的分佈函數。分佈相同就是分佈函數相同, 也可說有共同的分佈。
例 5. 投擲一公正的銅板三次, 令 表所得之正面數, 表所得之正面數,
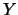 表所得之反面數。則 表所得之反面數。則 當然不等於 當然不等於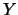 ( (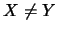 )。因若 )。因若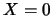 則 則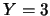 。事實上, 可看出 。事實上, 可看出
 與 與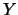 二者永不相等,
即 二者永不相等,
即
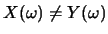 , ,
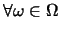 ,
其中 ,
其中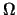 如例2. 5所給(如當 如例2. 5所給(如當
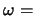 正正正,
則 正正正,
則
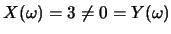 )。但因 )。但因
故 與 與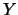 有相同的分佈函數, 即 有相同的分佈函數, 即
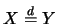 。 。
雖
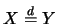 時不一定導致 時不一定導致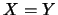 ,
但 ,
但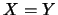 卻必導致 卻必導致
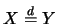 。此因 。此因
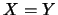 表 表
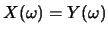 , ,
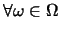 , 故 , 故
對一隨機變數 , 除了伴隨分佈函數 , 除了伴隨分佈函數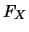 ,
亦有一與其關係密切的函數, 即機率密度函數(probability
density function, 縮寫為p.d.f.), 或是機率質量函數(probability
mass function, 縮寫為p.m.f.),
前者是對連續型, 後者是對離散型。不過為了簡便,
通常我們不分連續或離散, 皆說是機率密度函數。 ,
亦有一與其關係密切的函數, 即機率密度函數(probability
density function, 縮寫為p.d.f.), 或是機率質量函數(probability
mass function, 縮寫為p.m.f.),
前者是對連續型, 後者是對離散型。不過為了簡便,
通常我們不分連續或離散, 皆說是機率密度函數。
例 6. 設隨機變數 之機率密度函數為 之機率密度函數為
求(i)其分佈函數為何?
(ii)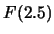 = ? = ? 
離散型機率密度函數之圖形, 有時以線段表之。
而對只取整數值之隨機變數, 其機率密度函數的圖形,
有時以一些小長方形表示, 每一小長方形之底部中點為取值處,
高度為該點之機率, 因此小長方形面積和為1。
這樣表示機率密度函數的圖形, 稱為直方圖(histogram),
機率便對應直方圖之面積。例 7中之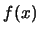 亦可繪成如圖4.5中之二圖,
右圖即直方圖。 亦可繪成如圖4.5中之二圖,
右圖即直方圖。
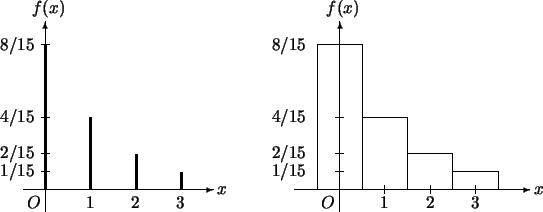
圖4.5 例 7中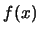 之圖形 之圖形
(連續型)若 為連續型,
則其機率密度函數的定義為滿足下式之非負函數 為連續型,
則其機率密度函數的定義為滿足下式之非負函數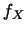 (稍後在例 9會指出 (稍後在例 9會指出 並不唯一): 並不唯一):
|
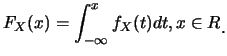
|
(4.7)
|
由定理4.1, 因
故知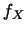 除了非負之外, 尚須滿足 除了非負之外, 尚須滿足
|
對連續型的隨機變數 , 由於 , 由於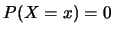 , ,
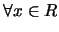 ,
即 ,
即 取任一定值的機率為0。故 取任一定值的機率為0。故
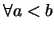 。 。
例 7. 設隨機變數 之分佈函數為 之分佈函數為
求
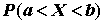 之值。
之值。 
由微積分基本定理(Fundamental Theorem of Calculus),
若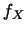 為連續函數, 則由(4.7)式, 為連續函數, 則由(4.7)式,
|
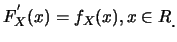
|
(4.9)
|
可藉由上式得到此時之機率密度函數。又二隨機變數,
若有相同的機率密度函數, 則其分佈相同。
例 8. 設隨機變數 之分佈函數 之分佈函數
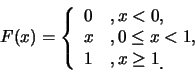
。則其機率密度函數為何? 
例 9.考慮標準的羅吉斯分佈, 即
則其機率密度函數為何? 
一函數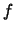 若滿足 若滿足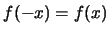 , ,
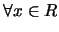 , 便稱為偶函數(even function)。偶函數之圖形對稱於 , 便稱為偶函數(even function)。偶函數之圖形對稱於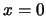 。
若存在一常數 。
若存在一常數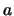 , 使得 , 使得
|
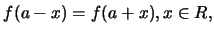
|
(4.11)
|
或等價地
|
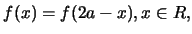
|
(4.12)
|
便說
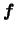 對稱於 對稱於
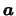 。即若一隨機變數之p.d.f.對稱於 。即若一隨機變數之p.d.f.對稱於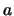 ,
便稱其分佈對稱於 ,
便稱其分佈對稱於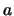 。分佈函數 。分佈函數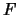 若滿足 若滿足
|
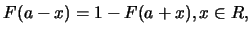
|
(4.13)
|
或等價地
|
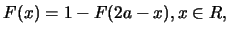
|
(4.14)
|
便稱分佈對稱於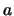 。函數 。函數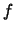 若滿足 若滿足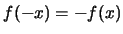 , ,
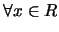 , 便稱為奇函數(odd function)。 , 便稱為奇函數(odd function)。
連續型的分佈不一定有機率密度函數,
此因一連續函數不一定可微。
對連續型的隨機變數, 除非特別聲明, 我們均假設其機率密度函數存在。
例 10. 設函數
(i)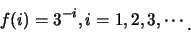
(ii)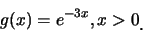
是否為機率密度函數? 
對一隨機變數 , 以 , 以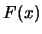 為分佈函數, 為分佈函數, 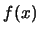 為機率密度函數,
有時可以 為機率密度函數,
有時可以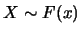 或 或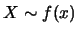 表之。若 表之。若
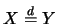 , 也可以 , 也可以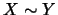 表之。對一隨機變數,
給定其機率密度函數, 或分佈函數,
或其他可以唯一決定其機率如何分配的規則,
皆稱為給定其分佈。 表之。對一隨機變數,
給定其機率密度函數, 或分佈函數,
或其他可以唯一決定其機率如何分配的規則,
皆稱為給定其分佈。
給一非負的函數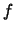 , 只要其圖形與 , 只要其圖形與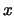 軸間之面積為1,
便是一機率密度函數。最簡單的機率密度函數,
是在一有限的區間中為常數。即設有一區間 軸間之面積為1,
便是一機率密度函數。最簡單的機率密度函數,
是在一有限的區間中為常數。即設有一區間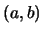 , , 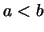 ,
且 ,
且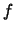 在該區間為一常數。即 在該區間為一常數。即
具有這種機率密度函數的隨機變數, 稱為在區間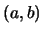 有均勻分佈(uniform distribution), 以 有均勻分佈(uniform distribution), 以
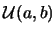 表之。 表之。
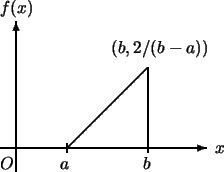
例 11. 考慮如圖4.9之函數 的圖形, 其中 的圖形, 其中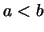 , 且 , 且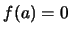 , ,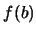 = =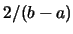 。求其機率密度函數及分怖函數。 。求其機率密度函數及分怖函數。 
圖4.9 例 12中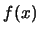 之圖形 之圖形
例 12. 假設我們希望圖4.10中之圖形為一機率密度函數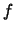 的圖形。則機率密度函數 的圖形。則機率密度函數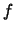 為何 ? 為何 ? 
圖4.10 例4.13中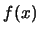 之圖形 之圖形
例 13. 設隨機變數 之機率密度函數為 之機率密度函數為
圖4.11給出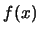 之圖形。 之圖形。
圖4.11 例 14中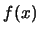 之圖形 之圖形
求 之機率. 之機率. 
對連續型的隨機變數, 不只機率密度函數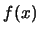 的值可大於1, 的值可大於1,
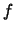 也可不為有界(bounded)。所謂有界即存在一常數 也可不為有界(bounded)。所謂有界即存在一常數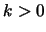 ,
使得 ,
使得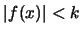 , ,
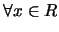 。 。
例 14. 設隨機變數 之機率密度函數為 之機率密度函數為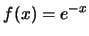 , , 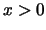 。求 。求 (i)
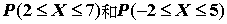 之值。 之值。
(ii)分佈函數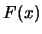 何? 何? 
進一步閱讀資料:黃文璋 (2003) . 基本概念。數理統計講義第一章。國立高雄大學應用數學系。
  
|
|
|
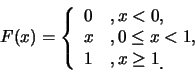
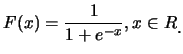

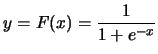 ,
, 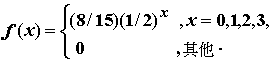
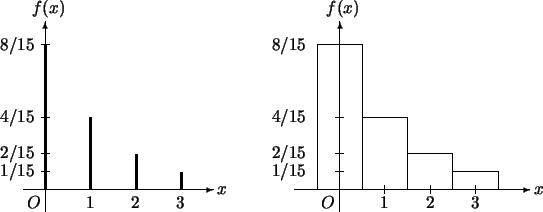
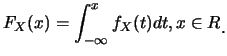
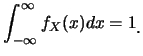
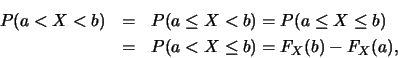
(60.5,20)(60.5,59)
\put(50,65){$(8,c)$}
\end{picture}](img239.gif)