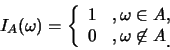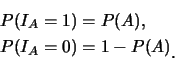|
  
隨
機 變 數
對於隨機變數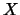 , 可以想成原先觀測到 , 可以想成原先觀測到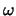 , 再轉換至 , 再轉換至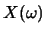 ,
樣本空間由 ,
樣本空間由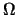 轉為 轉為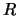 。
但也可想成所觀測到的結果就是 。
但也可想成所觀測到的結果就是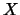 。 。
隨機變數定義於樣本空間,
樣本空間中的元素之出現情況是隨機的, 以一機率函數來描述。
由於在樣本空間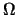 上, 上,
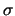 -體 -體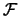 選取的不同,
使得並非每一由 選取的不同,
使得並非每一由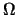 映至 映至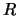 的函數, 皆可當做隨機變數。一般要求還要滿足 的函數, 皆可當做隨機變數。一般要求還要滿足
|
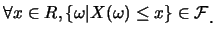
|
(3.1)
|
隨機變數常以大寫的英文字母表示,
而它的觀測值則以對應的小寫字母表示。有時會說``
隨機變數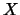 取值 取值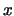 '', 或說`` 求 '', 或說`` 求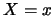 之機率''。 之機率''。
假設樣本空間
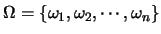 ,
取 ,
取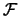 為包含 為包含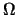 之所有子集合所形成的 之所有子集合所形成的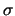 -體。定義一隨機變數 -體。定義一隨機變數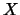 ,
其值域以 ,
其值域以
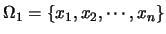 表之。則會觀測到 表之。則會觀測到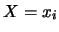 , 若且唯若原試驗的結果為 , 若且唯若原試驗的結果為
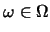 ,
使得 ,
使得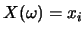 。即 。即
|
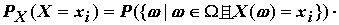
|
(3.2)
|
為了簡便, 常簡單地寫成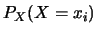 。(3.2)式之左側函數 。(3.2)式之左側函數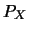 ,
就是由原機率函數引發出來的定義在 ,
就是由原機率函數引發出來的定義在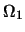 上的機率函數, 上的機率函數,
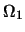 為新的機率空間, 且 為新的機率空間, 且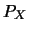 的確滿足柯莫果洛夫公理。雖然 的確滿足柯莫果洛夫公理。雖然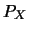 與 與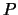 為不同的函數, 但因有(3.1)式,
今後如果不會混淆, 我們通常只寫 為不同的函數, 但因有(3.1)式,
今後如果不會混淆, 我們通常只寫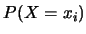 , 且將 , 且將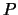 解釋為`` 機率
''的意思。 解釋為`` 機率
''的意思。
例 1. 投擲一銅板3次, 樣本空間 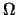 ={正正正,正正反,正反正,反正正,正反反,反正反,反反正,反反反}, ={正正正,正正反,正反正,反正正,正反反,反正反,反反正,反反反},
且設每一樣本之機率為1/8。
令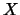 表共得之正面數。顯然 表共得之正面數。顯然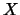 之值域為 之值域為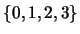 。則 。則
同理可得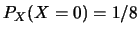 , , 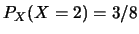 , , 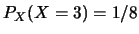 。 。
次令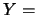 正面數 正面數 反面數。則Y 之值域為 反面數。則Y 之值域為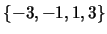 。且 。且
同理可得
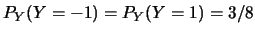 , , 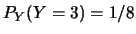 。 。
例 2. 投擲一公正的銅板100次,
則樣本空間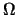 中共有 中共有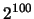 個元素。由於此銅板為公正,
所以每個樣本點之機率均相同, 皆為 個元素。由於此銅板為公正,
所以每個樣本點之機率均相同, 皆為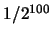 。令 。令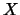 表所得之正面數。欲求 表所得之正面數。欲求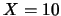 之機率。 之機率。 
一般而言, 令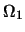 表隨機變數 表隨機變數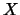 所引發出來的樣本空間,
則對 所引發出來的樣本空間,
則對
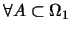 , 我們定義引發出來的機率函數 , 我們定義引發出來的機率函數
例 3. 如果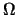 本來就是實數的一個子集合,
則 本來就是實數的一個子集合,
則
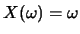 為一很自然的隨機變數。例如,
一袋中有10張紙牌, 分別寫數字1至10。隨機地取一張,
觀測所得之點數。則樣本空間 為一很自然的隨機變數。例如,
一袋中有10張紙牌, 分別寫數字1至10。隨機地取一張,
觀測所得之點數。則樣本空間
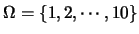 。可令 。可令
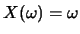 , 而得一隨機變數。另一種講法是自袋中隨機地取一張紙牌, 並令 , 而得一隨機變數。另一種講法是自袋中隨機地取一張紙牌, 並令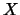 表所得之點數。這種講法就是直接引進隨機變數。 表所得之點數。這種講法就是直接引進隨機變數。
常數也是一隨機變數。對一實數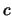 , 若 , 若
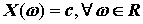 , 則
, 則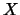 為一隨機變數。有時以 為一隨機變數。有時以
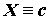 表之。
這種只取一個值之隨機變數, 由於並不會變, 雖然仍視為隨機變數,
但稱之為退化的(degenerate)。
表之。
這種只取一個值之隨機變數, 由於並不會變, 雖然仍視為隨機變數,
但稱之為退化的(degenerate)。
例 4. 設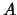 為樣本空間 為樣本空間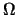 之一子集.令 之一子集.令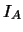 表 表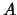 之指示函數(indicator function), 即若 之指示函數(indicator function), 即若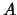 發生, 則 發生, 則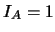 , 否則 , 否則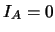 。 。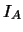 便是``
指示'' 事件 便是``
指示'' 事件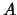 是否發生。因此 是否發生。因此
則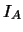 為一隨機變數, 它只取1與0兩個值, 且 為一隨機變數, 它只取1與0兩個值, 且
利用指示函數, 可將每一事件對應一隨機變數。
進一步閱讀資料:黃文璋 (2003) . 基本概念。數理統計講義第一章。國立高雄大學應用數學系。
  
|