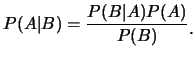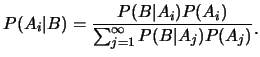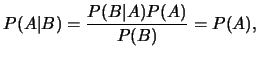|
  
條件機率與獨立性
有時得到一些資訊,
則根據所獲得的資訊, 要修訂樣本空間, 因而機率空間可能也會改變。這就是所謂條件機率(conditional
probability)。
在條件機率的定義中, 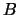 成為新的樣本空間: 成為新的樣本空間:  。所有事件發生之機率,
都要先將其針對與 。所有事件發生之機率,
都要先將其針對與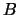 的關係做修正。 的關係做修正。
例 1. 在梭哈遊戲裡, 要拿到四條的機率很低。但若發了三張牌, 皆拿到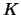 , 則此時會拿到四條之機率為何? , 則此時會拿到四條之機率為何? 
由(2.1)式得
|
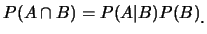
|
(2.2)
|
故若知道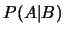 及 及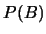 , 則可得到 , 則可得到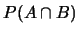 。當然亦有 。當然亦有
|
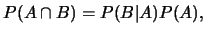
|
(2.3)
|
只要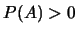 。結合(2.2)與(2.3)式, 得 。結合(2.2)與(2.3)式, 得
|
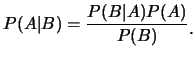
|
(2.4)
|
(2.4)式為貝氏定理(Bayes' Rule)之一特例。
定理 1. 設
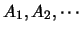 為某樣本空間之一分割.則對任一事件 為某樣本空間之一分割.則對任一事件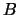 , ,
|

|
(2.5)
|
|
例 2. 有甲、乙、丙三囚犯, 國王以抽籤決定釋放其中一位,
處決另兩位。然後他告訴獄卒那一位將被釋放,
但要求獄卒不可先透露。甲先是要求獄卒告訴他那一位會被釋放,
遭到拒絕後, 改為問獄卒, 乙,丙中那一位會被處決。獄卒經過一番思考,
遂告訴甲, 乙會遭處決。他認為這樣做並未違反國王的規定,
原因為:
乙、丙二人, 至少有一會遭處決,
因此他並未提供甲有關甲是否會被釋放的有用資訊。
甲聽到獄卒說乙會被處決後很高興。原先他只知道自己有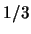 的機會遭釋放, 現因只剩他與丙了,
所以他會被釋放的機會提高至 的機會遭釋放, 現因只剩他與丙了,
所以他會被釋放的機會提高至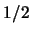 。 。
究竟獄卒與甲誰的分析, 何者才是正確的呢? 
定義 2.二事件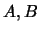 , 稱為相互獨立(mutually independent, 簡稱獨立),
若滿足 , 稱為相互獨立(mutually independent, 簡稱獨立),
若滿足
|
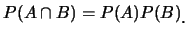
|
(2.7)
|
|
在討論條件機率時, 有時事件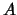 之發生,
對事件 之發生,
對事件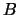 之發生的機率沒有影響。即 之發生的機率沒有影響。即
|
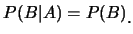
|
(2.8)
|
又由(2.4)式得
|
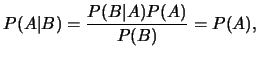
|
(2.9)
|
在(2.8)及(2.9)二式中,
分別要有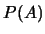 , 及 , 及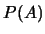 與 與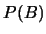 為正的條件。不過(2.7)式對 為正的條件。不過(2.7)式對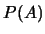 或 或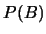 為0仍成立。以(2.7)式當做 為0仍成立。以(2.7)式當做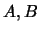 獨立的條件。 獨立的條件。
當事件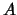 與 與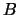 獨立時, 由 獨立時, 由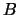 之發生, 對事件 之發生, 對事件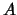 得不到任何推論(inference)。因此直觀上 得不到任何推論(inference)。因此直觀上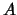 與 與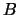 獨立,
會導致 獨立,
會導致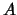 與 與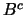 獨立。 獨立。
例 3. 投擲一公正的骰子兩次, 則樣本空間為
共包含36個元素, 其中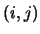 表第一次出現點數 表第一次出現點數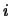 ,
第二次出現點數 ,
第二次出現點數 。取 。取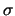 -體為包含 -體為包含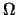 所有子集合之集合(共有 所有子集合之集合(共有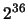 個元素)。令 個元素)。令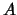 表兩次投擲出現的點數相同, 表兩次投擲出現的點數相同, 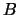 表兩次投擲點數和介於7與10間, 表兩次投擲點數和介於7與10間,
 表兩次投擲點數和為2,7或8。因此, 表兩次投擲點數和為2,7或8。因此,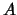 , ,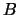 與 與 是否相互獨立? 是否相互獨立? 
由定義 3, 一般而言, n
個事件要相互獨立, 就須有

個等式成立。
例 4. 考慮投擲一銅板三次的試驗。令`` 正正反''
表頭兩次出現正面, 第三次出現反面, 餘類推。則樣本空間為 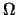 ={正正正,正正反,正反正,反正正,正反反,反正反,反反正,反反反}。 ={正正正,正正反,正反正,反正正,正反反,反正反,反反正,反反反}。
對每一樣本點給定機率1/8。又令 表第 表第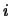 次投擲得到正面之事件。則 次投擲得到正面之事件。則
同理
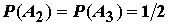 。 試驗證對此機率模型,
事件
。 試驗證對此機率模型,
事件
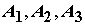 為相互獨立。
為相互獨立。 
例 5. 假設生男與生女的機率均為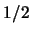 。若一家庭中有兩個小孩,
已知其中之一為男孩, 試求另一為女孩之機率。 。若一家庭中有兩個小孩,
已知其中之一為男孩, 試求另一為女孩之機率。 
例 6. 在上例中, 若亦知該男孩為老大, 試回答同樣的問題。

進一步閱讀資料:黃文璋 (2003) . 基本概念。數理統計講義第一章。國立高雄大學應用數學系。
  
|