

微分方程式之級數解
a
級數
在其收斂區間定義出一函數。對一微分方程式,
有時也可藉由級數來表示其解。見下例。
例 1.求 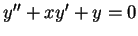 之一級數解。
之一級數解。 
對一微分方程式
若 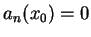 , 則
, 則 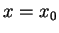 稱為此微分方程式之一奇異點 。級數的解只在不包含
稱為此微分方程式之一奇異點 。級數的解只在不包含 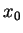 的區間存在。
的區間存在。
例 2.試解
一函數若在某區間中可表示成一冪級數, 則稱此函數在該區間中為解析的, 上述作法便是找一微分方程式之解析解。我們給下述定理。
利用級數解也可證明唯一性定理 。 設 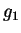 及
及 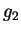 為
為
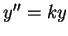 之二解, 且滿足
之二解, 且滿足
其中
![$x_0\in [x_1, x_2]$](img61.gif) 。令
。令
則 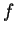 仍為
仍為 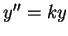 之一解, 且
之一解, 且
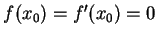 。因
。因
即對
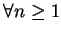 ,
,
由定理 1 ( 即 (7.1) 式),
而此冪級數之每一係數皆為 0, 故 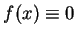 ,
,
![$\forall x\in [x_1,x_2]$](img45.gif) 。因此
。因此
換句話說, 由給定起始條件當 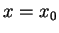 時,
時, 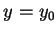 ,
, 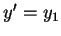 ,
可唯一決定
,
可唯一決定 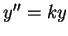 之解。
之解。
進一步閱讀資料:黃文璋(2002).
微分方程式之級數解。微積分講義第十一章,國立高雄大學應用數學系。

