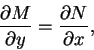恰當微分方程式

  a

        本節我們來看另一類可解的一階線性微分方程式。首先一微分方程式

\begin{displaymath} M(x,y)+N(x,y)y'=0, \end{displaymath}

(5.1)

若滿足

\begin{displaymath} \frac {\partial M}{\partial y}=\frac {\partial N}{\partial x}, \end{displaymath}

便稱為恰當微分方程式。可看出 (4.1) 之可分離微分方程式亦為一種恰當微分方程式。不過除非 $M(x,y)$ 僅為一 $x$ 之函數, 且 $N$ 僅為一 $y$ 之函數, 否則一恰當微分方程式並不為一可分離的微分方程式。

　　設有一方程式 。因

\begin{displaymath} \frac {\partial }{\partial y}(2x-y)=-1=\frac {\partial }{\partial x}(y^2-x), \end{displaymath}

故此為一恰當微分方程式。

　　底下我們皆設 (5.1) 中之 與 $N$ 有連續的一階偏導數。

定理 1.設 $F(x,y)$ 之二一階偏導數皆連續, 且

\begin{displaymath} \bigtriangledown F=(M, N), \end{displaymath}

(5.2)

則

\begin{displaymath} F(x,y)=C, \end{displaymath}

(5.3)

其中 $C$ 為一常數, 為恰當微分方程式

\begin{displaymath} M(x,y)+N(x,y)y'=0 \end{displaymath}

(5.4)

之一般解。                                                                               證明

  a

例 1.試解

\begin{displaymath} 2x-y+(y^2-x)y'=0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}   


例 2.試解

\begin{displaymath} \sin y+(x\cos y+y\cos y+\sin y)y'=0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}  

　

　　最後, 對一可分離微分方程式 (4.1), 即

\begin{displaymath} Q(x)-A(y)y'=0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

仿上述解法, 可得 為解, 而此即 (4.2) 式。 此為定理 1 之另一證明。 又附帶一提, (5.1) 式有時也寫成

\begin{displaymath} M(x,y)dx+N(x,y)dy=0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(5.9)


     

  a  a

進一步閱讀資料：黃文璋(2002). 恰當微分方程式。微積分講義第十一章，國立高雄大學應用數學系。