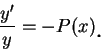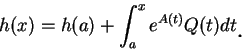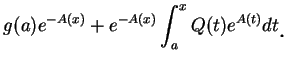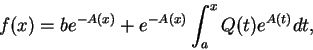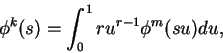一階線性微分方程式

  a      

　　在第五章定理 4.1 我們已證出 $y$ 滿足

\begin{displaymath} y'=\alpha y, \end{displaymath}

(2.1)

若且唯若

\begin{displaymath} y=Ce^{\alpha x}, \end{displaymath}

其中 $C$ 為一常數。因 $x=0$ 時 $y=C$, 故 $C$ 可由給定 $x=0$ 時, $y$ 之值決定。

　　上述結果就是一存在且唯一性定理之例。在給定起始條件下, (2.1) 式存在一解 , 且最多也只有一解。微分方程式中的許多研究, 便是找出某類方程式存在且唯一的定理。底下我們來討論一重要形式的 微分方程式的解, 此形式為 (2.1) 之一推廣。

　　設 $P$、$Q$ 為二給定的方程式, 則

\begin{displaymath} y'+P(x)y=Q(x), \end{displaymath}

(2.2)

便稱為一階線性微分方程式 。(2.2) 中之 $y$ 為一待解之 $x$ 的函數, $P$、$Q$ 假設在某一開區間 $I$ 中為連續, 我們便是想求在 $I$ 中之所有的解 $y$。由於 (2.2) 中 $y$ 之導數為一階, 且 $y'$ 可視為一 $y$ 之線性函數: $y'=-P(x)y+Q(x)$, 所以會如此命名。這是一類形式簡單但很重要的微分方程式。一般而言, 一微分方程式中的各導數若皆為一次, 便稱為線性的。如

\begin{displaymath} a_0(x)y^{(n)}+a_1(x)y^{(n-1)}+\cdots+a_{n-1}(x)y'+ a_n(x)y=Q(x)\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

而若 $a_0(x),a_1(x),\cdots,a_n(x)$ 皆為常數, 便稱為常係數線性微分方程式。

　　我們先看一特例, 即 $Q(x)\equiv 0$ 的情況, 此時

\begin{displaymath} y'+P(x)y=0, \end{displaymath}

(2.3)

稱為對應 (2.2) 之一齊性方程式。我們先導出齊性方程式的解, 然後藉此得到 (2.2) 之非齊性方程式的解。

　　若在 $I$ 中 $y\neq 0$, 則 (2.3) 式等價於下式:

\begin{displaymath} \frac {y'}{y}=-P(x)\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(2.4)

現設 $y$ 為一滿足 (2.4) 之正函數, 則 (2.4) 成為

\begin{displaymath} \frac {d}{dx}(\log y)=-P(x), \end{displaymath}

由此即得

\begin{displaymath} \log y=-\int P(x)dx+C\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

因此

\begin{displaymath} y=e^{-A(x)},\ \ \mbox{其中}\ \ A(x)=\int P(x)dx-C\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(2.5)

亦即若 (2.3) 有一正的解, 則必為 (2.5) 的形式。 $e^{-A(x)}$ 稱為 (2.3) 之一積分因子。另外, 也可如下地證明每一由 (2.5) 所定義出之函數必為 (2.3) 式之解:

\begin{displaymath} y'=-A'(x)e^{-A(x)}=-P(x)e^{-A(x)}=-P(x)y\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

因此我們即求出所有滿足 (2.3) 之正的 $y$。底下我們給出 (2.3) 式之所有解, 且將結果敘述為一存在且唯一的定理。

定理 1.設函數 $P$ 在開區間 $I$ 連續。自 $I$ 中任取一點 $a$, 且令 $b$ 為任一實數。則存在唯一的函數 $y=f(x)$, 滿足

(2.6)

又此函數為                                                                                                           證明

(2.7)

 

　　由上定理證明中的最後一部分, 即提供一解非齊性微分方程式 (2.2) 的方法。設 $g$ 為滿足 (2.2) 之任一解, 且令 $h(x)=g(x)e^{A(x)}$, 其中 $A(x)=\int_a^x P(t)dt$。則 (2.9) 仍成立。又因 $g$ 滿足 (2.2), $g'(x)+P(x)g(x)=Q(x)$, 故此時

\begin{displaymath} h'(x)=e^{A(x)}Q(x)\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

再由微積分基本定理的第二部分得

\begin{displaymath} h(x)=h(a)+\int_a^x e^{A(t)}Q(t)dt\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

又因 $h(a)=g(a)$, 故每一滿足 (2.2) 之解必有下述形式:

$\displaystyle g(x)$

$\textstyle =$

$\displaystyle e^{-A(x)}h(x)$

(2.10)

 

$\textstyle =$

$\displaystyle g(a)e^{-A(x)}+e^{-A(x)}\int_a^x Q(t)e^{A(t)}dt\mbox{\raisebox{-1.2mm}{\large . }}$

 

反之, 經由直接對 (2.10) 式微分, 易見 (2.10) 所定義出之函數為 (2.2) 之一解。我們便找出了滿足 (2.2) 之所有解。我們將結果敘述如下。

　

定理 2.設 $P$、$Q$ 為二在開區間 $I$ 上連續的函數。任取一 $a\in I$, 且令 $b$ 為任一實數。則恰有一函數 $y=f(x)$, 滿足

(2.11)

又此函數為

\begin{displaymath} f(x)=be^{-A(x)}+e^{-A(x)}\int_a^x Q(t)e^{A(t)}dt, \end{displaymath}

(2.12)

其中 $A(x)=\int_a^x P(t)dt$。 

  a
例 1.求

\begin{displaymath} xy'+(1-x)y=e^{2x},\ x\in (0,\infty ), \end{displaymath}

之所有解。 


例 2.微分方程式

\begin{displaymath} y'+R(x)y=S(x)y^k,\ \ k\neq 0, 1, \end{displaymath}

(2.13)

稱為 Bernoulli 方程式 。此為 Jacob Bernoulli 在西元 1695 年所提出。求其解。 

　　
例 3.解

\begin{displaymath} y'+\frac 1 x y=x^5y^4\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}   

例 4.設 $C_1, C_2\neq 0$, 求一 $y=f(x)$, 且 $y\neq 0$, 滿足

\begin{displaymath} y'+C_1y^2+C_2 y=0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(2.14)

　　有些方程式要經適當地轉換, 才會成為一微分方程式。如在下例中, 原來給的是一積分方程式, 但經幾次轉換後, 便得到一常見形式之微分方程式。


例 5.設函數 $\phi(s)$ 定義在 $s\geq 0$, 且滿足

\begin{displaymath} \phi^k(s)=\int_0^1 ru^{r-1}\phi^m(su)du, \end{displaymath}

(2.15)

其中 $m>k$, $r>0$。試證存在一 $\lambda\geq 0$, 使得

\begin{displaymath} \phi(s)=(1+\lambda s^c)^{-1/(m-k)}, \end{displaymath}

(2.16)

其中 $c=r(m-k)/k$。 


例 6.試證

\begin{displaymath} x+\frac 2 3 x^3+\frac 2 3\frac 4 5 x^5+\frac 2 3\frac 4 5 \f... ...{\arcsin x} {\sqrt {1-x^2}}\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}  

          a  a

進一步閱讀資料：黃文璋(2002). 一階線性微分方程式。微積分講義第十一章，國立高雄大學應用數學系。