|
  
可分離的微分方程式
a
微分方程式
若
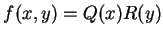 , 便稱此為一階之可分離微分方程式。諸如, , 便稱此為一階之可分離微分方程式。諸如, 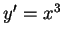 , ,
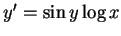 皆為可分離之微分方程式。若 皆為可分離之微分方程式。若 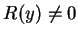 , 則 , 則
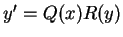 可改寫為 可改寫為
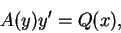 |
(4.1) |
其中  。下述定理給出可分離的微分方程式之解。 。下述定理給出可分離的微分方程式之解。
a
(4.2) 式亦可以 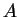 來表示。由 (4.3) 得 來表示。由 (4.3) 得
在上式中, 若令 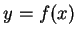 , 則 , 則 , 即得 , 即得
 |
(4.5) |
因 為 為 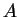 之一反導數, 故上式為 (4.2)
式之另一寫法。事實上, 由 (4.1) 直接得到 (4.5)
為萊布尼茲符號之有效性的另一佐證。我們可在 (4.1) 中, 先將 之一反導數, 故上式為 (4.2)
式之另一寫法。事實上, 由 (4.1) 直接得到 (4.5)
為萊布尼茲符號之有效性的另一佐證。我們可在 (4.1) 中, 先將 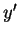 寫成
寫成 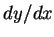 , 然後將 , 然後將 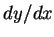 假設為 假設為  除以 除以  , 再兩側各乘以 , 再兩側各乘以
 得
最後, 左、右各附上一積分符號, 右側加上一常數便得 (4.2) 式。這種方式常常行得通, 彷彿定理 4.1 中之證明皆為多餘。 得
最後, 左、右各附上一積分符號, 右側加上一常數便得 (4.2) 式。這種方式常常行得通, 彷彿定理 4.1 中之證明皆為多餘。
例 1.試解
例 2.試解
a
進一步閱讀資料:黃文璋(2002).
可分離的微分方程式。微積分講義第十一章,國立高雄大學應用數學系。
  
|