一、連續
期恰有(至少有)1碼相同之機率
1.
恰有：
至少有：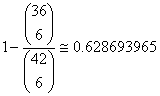
2.
恰有：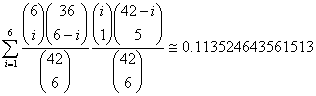
至少有：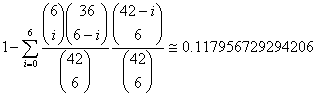
3.
恰有：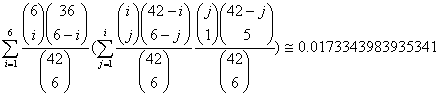
至少有：
4.
恰有：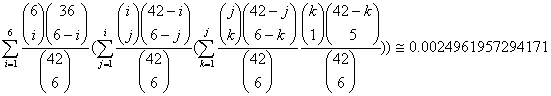
至少有：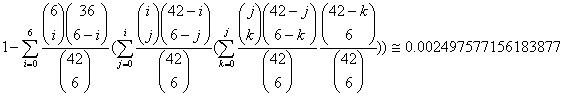
二、連號之機率
依連號情況，共有下述可能：
1. 6
2. 51
3. 42
4. 411
5. 33
6. 321
7. 3111
8. 222
9. 2211
10. 21111
11. 111111
註1. 6表6連號，51表5連號及另一個不相連號碼，餘類推；42與24相同，餘類推；又111111表沒有連號。
註2. 4連號並不視為一種三連號，及兩組二連號，餘類推。
|
事件 |
事件之組合數 |
事件之機率 |
|
6 |
37(A) |
0.000007053280481 |
|
51 |
1,332(B) |
0.0002539180973 |
|
42 |
1,332(C) |
0.0002539180973 |
|
411 |
23,310(D) |
0.004443566703 |
|
33 |
666(E) |
0.0001269590487 |
|
321 |
46,620(F) |
0.008887133406 |
|
3111 |
264,180(G) |
0.050360422 |
|
222 |
7,770(H) |
0.001481188901 |
|
2211 |
396,270(I) |
0.075540633 |
|
21111 |
2,179,485(J) |
0.415473486 |
|
111111 |
2,324,784(K) |
0.443171719 |
|
有連號 |
2,921,002(=A+B+C+D+E+F+G+H+I+J) |
0.55682828 |
|
至少一組四連號 |
24,642(=C+D) |
0.0046974848 |
|
至少一組三連號 |
311,466(=E+F+G) |
0.059374515 |
|
至少一組二連號 |
2,631,477(C+F+H+I+J) |
0.501636361 |
|
至少二組二連號 |
404,040(=H+I) |
0.077021822 |
註3. A+B+C+D+E+F+G+H+I+J+K=5,245,786
三、最小間距(Minimum Gap,簡寫為MG)及總間距數之機率分佈
這裡所謂的最小間距，是指一組號碼經過排序後，兩相鄰號碼間距的最小值，以
MG
表示。假設從
1, …, N
的號碼中挑選出
n
個號碼
，排序之後的結果為
，則最小間距定義如下：
。
由於知
之組合數有
種，所以
的機率值
，
。
由此即得 MG = l 的機率為
，
。
上述之結果，在Haigh(1995), Kennedy and Cooper(1991), Speckman(1991), 及Boland, P. J. and Pawitan, Y. (1999)等文章中，都曾經提及。
底下簡單地說明如何得到
的組合數。
首先我們考慮一連續數列{1,
2, …, N-(l-1)(n-1)}，想要從中挑選n個號碼,
則依據排列組合的概念，共有
種選擇方式。令
是其中的一種選法，且定義 
, 
,…, 
。因此, 我們不難看出
,
，且
的值會落在{1, 2, …,
N}中。換句話說
是從{1, 2, …,
N}挑出的
n個號碼，且相鄰二數之間距至少為
l。這也就是我們想要的
事件。
另外,
因為
是由
定義而來, 所以有1對1的關係。因此,
根據上述之結果得知，
會有
種組合數。證畢。
MG = 1表示最小間距為1, 其另一個意義為至少會有一對連號。根據上述公式，若以台灣樂透彩42取6為例，則
，
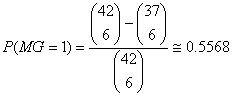即連號機率約為0.5568。將不同MG之機率值整理如下：
|
MG = l |
組合數 |
P (MG = l ) |
|
1 |
2,921,002 |
0.556828280833416 |
|
2 |
1,418,592 |
0.270425061182442 |
|
3 |
610,182 |
0.116318507846107 |
|
4 |
221,397 |
0.0422047334755936 |
|
5 |
62,237 |
0.0118641896562307 |
|
6 |
11,452 |
0.00218308562339371 |
|
7 |
917 |
0.00017480697840133 |
|
8 |
7 |
0.00000133440441527733 |
此外，在一組
n
個號碼的數列
中，會有
個間距。依據間距值可得知，此組號碼有幾種不同的間距。因此，針對每組號碼，我們定義一隨機變數如下：
，
表示此組號碼之總間距數。Henze, N. (1997) 提出S之機率分佈如下：
v
= 2,
3, …, n-1，其中
表第
種間距的大小，
則是
的個數，
，
。若S
= 1，即表示這6個號碼的間距只有1種，如：{1,
2, 3, 4, 5, 6}, {1, 3, 5, 7,9, 11}, …等。此類數列也就是我們熟知的等差數列。
根據上式，台灣樂透彩 S 之機率分佈如下表所示：
|
S = v |
組合數 |
P (S = v) |
|
1 |
156 |
0.0000297381555404662 |
|
2 |
27,540 |
0.00524992822810538 |
|
3 |
565,630 |
0.107825595630474 |
|
4 |
2,448,780 |
0.466808977720403 |
|
5 |
2,203,680 |
0.420085760265478 |
由此可知，S = 1對應等差數列，顯然極不易出現。
參考文獻
1. Boland, P. J. and Pawitan, Y. (1999), Trying to be Random in Selecting Random Numbers for Lotto, Journal of Statistical Education, 7, 3.
2. Haigh, N. (1995), Inferring Gambler's Choice of Combinations in the National Lottery, Bulletin of the Institute of Mathematics and its Applications, 31(9-10), 132-136.
3. Henze, N. (1997), A statistical and probabilistic analysis of popular lottery tickets, Statistica Neerlandica, 51(2), 155-163.
4. Kennedy, R. E., and Cooper, C. N. (1991), The Statistics of the Smallest Space on a Lottery Tickets, Fibonacci Quarterly, 29(4), 367-370.
5. Speckman, P. (1991), Lottery Loophole Explained, Stats, 5, 16.