接下來我們來看獨立性(independence)。 在機率論裡, 獨立是一很重要的概念。 不過這

種獨立的概念, 是所謂統計的獨立(statistically independent), 或稱隨機的獨立(stochastically  

independent), 與日常生活裡的主權獨立, 經濟獨立中的"獨立"意義並不相同。

    若一事件之發生, 對事件之發生的機率並沒有影響。即

                     , --------------------------------(1)

則我們說與相互獨立(mutually independent, 簡稱獨立)。此處需要求。

    再由先前介紹的條件機率知

                   ,--------------------------(2)

因此, 由(1)式與(2)式可得

                   。---------------------------(3)

(3)式對或為0時仍然成立(因此時(3)式左、右均為0)。所以我們就常以(3)式當

做與獨立的條件。採用(3)式的好處是將二事件與對稱地對待, 且較易推廣到超過

兩個事件獨立的情況。

    若要計算二獨立事件交集的機率, 我們只需將二事件個別的機率相乘即可。若要決定

與是否為獨立, 只要驗證是否成立, 若成立, 則與獨立, 

否則與相依(dependent)。

        當事件與 獨立時, 由 之發生, 對事件得不到任何推論(inference) 。因此直觀上 

 與 獨立, 會導致與獨立。這是正確的, 其推導如下:

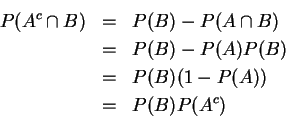
         \begin{eqnarray*} P(A^c\cap B) &=& P(B)-P(A\cap B)\\ &=& P(B)-P(A)P(B) (\mbox... ... A,B \mbox{為獨立事件})\\ &=& P(B)(1-P(A))\\ &=& P(B)P(A^c) \end{eqnarray*}

事實上不難看出, 與、與也都獨立。

    最後, 我們來看三個事件的獨立要如何定義?  

設 , , 為樣本空間中的三事件, 若滿足

   (1)  , , 兩兩獨立, 即

         ,

         , 

         ,

   (2) , 

則我們稱, , 三事件相互獨立(仍簡稱獨立)。

生活中的實例1

投擲一公正的骰子一次, 令表出現偶數點的事件, 表出現3點或6點的事件。試問與

是否獨立?

[解]: ={2,4,6}, ={3,6}, ={6}, 所以

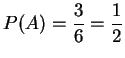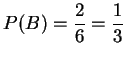     $P(A)=\displaystyle \frac 36=\frac 12$, $P(B)=\displaystyle \frac 26=\frac 13$,

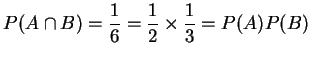     $P(A\cap B)=\displaystyle \frac 16=\frac 12\times \frac 13=P(A)P(B)$, 

所以事件與獨立。

　

隨堂練習1

投擲一骰子二次, 令$A$表第一次為4點的事件, $B$表第二次為3或6點的事件。試問與是否

獨立。

[解]:獨立。

　

生活中的實例2

設, 為樣本空間$\Omega$之二事件, 若$P(A)=0.4$, $P(A\cup B)=0.7$, $P(B)=x$, 

試求滿足下述條件之$x$之值。

(1)$A$與$B$為互斥事件,

(2)$A$與$B$為獨立事件。

[解]:

(1) 因$A$與$B$為互斥事件, 所以 $A\cap B=\emptyset$, 且, 故

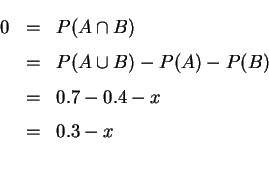
\begin{eqnarray*} 0 &=& P(A\cap B)\\ &=& P(A\cup B)-P(A)-P(B)\\ &=& 0.7-0.4-x\\ &=& 0.3-x\\ \end{eqnarray*}
　
    所以$x=0.3$。

(2) 因$A$與$B$為獨立事件, 故 , 因此可得

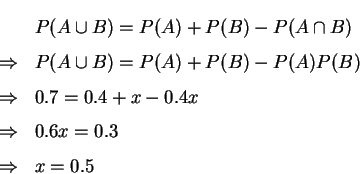
\begin{eqnarray*} && P(A\cup B)=P(A)+P(B)-P(A\cap B)\\ &\Rightarrow& P(A\cup B)... ... 0.7=0.4+x-0.4x\\ &\Rightarrow& 0.6x=0.3\\ &\Rightarrow& x=0.5 \end{eqnarray*}

　

隨堂練習2

甲乙二人平常射擊之命中率分別為0.5, 0.6, 且互不影響, 今有一鳥飛入射程內, 

二人同時各對他發射一槍, 求此鳥被命中之機率為何?

[解]: 0.8。

　

生活中的實例3

 某賣場經理根據過去經驗知道, 有80%的顧客在結帳時會使用信用卡, 則連續三位顧客皆使用

信用卡的機率為何? 

[解]: 在沒有其他已知的條件下, 我們假設此三位顧客使用信用卡的事件為獨立似不為過。因

此三人皆使用信用卡的機率為0.8×0.8×0.8=0.512。

　

隨堂練習3     

投擲一公正銅板三次, 令 $A$ 表第一次出現正面的事件, $B$表第二次出現正面的事件, 表第三次

出現反面的事件, 試問, , 三事件是否相互獨立。

[解]: , , 三事件相互獨立。

　

1. 在梅莉史翠普(Meryl streep)主演的越戰獵鹿人(The Deer Hunter, 1978年奧斯卡金像

獎最佳影片)那部電影裡,有一描述虐待戰俘的方法。在一可裝6發子彈的左輪手槍(revolver)

裡,只放一顆子彈,隨機地一轉後,要二戰俘輪流用手槍向自己的頭部發射,直到一名戰俘中槍,

另一名戰俘才逃過一劫。這就是所謂俄羅斯輪盤(Russian roulette)的遊戲。試問


(1) 先發射者是否較不利? 


(2) 若改為放兩顆子彈,結果有何不同? 

[解答部分]

1. (1) 無論先發射或後發射死亡機率均為0.5。

   (2) 對先發射者較不利。 

　

  1. 某一團體中有4位大一男生, 6位大一女生, 6 位大二男生, 及$x$位大二女生。若自此

    團體中任取一位學生, 其性別與年級獨立, 試問此時$x$為何值?

  2. 投擲一公正的骰子一次, 令$A$表得到偶數, 表得到奇數, 表得到7點, 試問此三事

    件是否獨立, 為什麼?

  3. 投擲一公正的骰子二次, 令$A$表第一次得到奇數, 表第二次得到奇數, 表兩次之和為

    奇數。試問此三事件是否獨立, 為什麼?

  4. 有一道數學題目, 甲生能解出之機率為0.5, 乙生能解出之機率為0.3, 若甲、乙二人同時

    解此道題目且互不影響, 試求下述情況之機率:

    (1) 甲、乙二人均解出,

    (2) 甲、乙二人恰有一人解出,

    (3) 甲、乙二人均未解出,

    (4) 此題被解出。

  5. 甲乙丙三人平常射擊之命中率分別為0.5, 0.6, 0.7, 且互不影響, 今有一鳥

    飛入射程內, 三人同時各對它發射一槍, 求此鳥被命中之機率為何?

　

[解答部分]

1. 9。

2. 不獨立, 因$A$與不獨立。

3. 不獨立。

4. (1) 0.15, (2)0.5, (3) 0.35, (4) 0.65。

5. 0.94。