在數學裡給定某個數是2, 它就一直是2。 但在機率裡, 某事件的機率是有可能因情況

而變。 這本來是不奇怪的, 但因大部分的人受數學的薰陶較久, 而數學裡通常是處理"不變"

的問題, 所以在學習機率時, 看到機率值居然會改變, 便不易理解。 如假設生男生女的機率

各為0.5。 則隨機抽取一個學生會是男或女的機率也就大約是0.5。但若知此學生是高雄女中

的學生, 則會是女生的機率就是1了, 因高雄女中沒有收男學生。 由於獲得資訊, 機率隨之而

變, 其實是合理的, 否則就失去收集資訊的目的。 

     若, 為樣本空間中二事件, 且。則在給定發生之下, 之條件機

率, 以表之, 定義為 

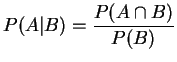                       。  ----------------------------(1)

在上述條件機率的定義中, 成為新的樣本空間: 。也就是原先的樣本空間

修正為。 所有事件發生之機率, 都要先將其針對與的關係做修正。 例如, 若與為互斥

事件,且, 則因, 故; 若亦為正, 則此時亦有

。

        條件機率也可用來求非條件下的機率。由(1)式得

                       。-------------------------(2)

故若知道及。 則可得到 。當然亦有

                      , --------------------------(3)  

只要。結合(2)式與(3)式, 得

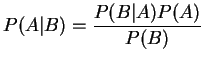                     。-----------------------------(4)

今後即使不特別聲明, 上式要成立就隱含著及皆為正。

(4)式為貝氏定理(Baye's Rule)之一特例, 這是英國牧師貝斯(Bayes, 1702-1761)所首先提出, 因

而命名。 不過也有人認為法國的大數學家拉普拉士(Laplace, 1749-1827)才是第一位明確給出此

定理者, 所以應稱為拉普拉士公式(Laplace's Formula)。

　

我們已知道 , 若樣本空間中, 還有一個事件,那

會有什麼樣的形式? 看看底下的推導: 

                。

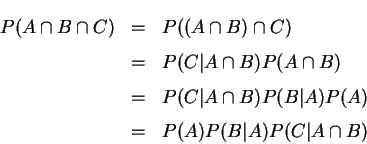似乎有點規律。 若樣本空間中, 再加一個事件, 不難看出有下列形式

         。

事實上, 我們可以給出更一般的形式, 設為樣本空間中的個事件, 且

, 則 

     

此即條件機率的乘法性質。除此之外, 條件機率還有一些基本性質, 我們分別列於下: 

 設,,為樣本空間中的任意三事件, 且設, 則有

(1) ,  , 

(2) ,

(3) ,

(4) ,

(5) 若, 則。

　

先前我們已給出貝氏定理之一特例, 現在我們給出一般的形式: 

設為樣本空間中之一分割(所謂分割就是 , , 

且)。 則對任意及任一事件, 只要, 

              。

例如, , 為樣本空間中之一分割, 在給定一事件, 且, 則

        。

                

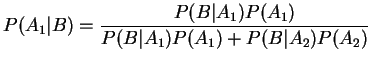生活中的實例1

 假設生男生女的機率相等。某家庭有兩個小孩, 試問

(1) 已知老大為男孩, 求老二為男孩的機率; 

(2) 已知有一男孩之下, 求兩個小孩均為男孩的機率。

[解]: 令表老大是男孩的事件, 表老二是男孩的事件, 所以

                    $A\cap B$表兩個小孩都是男孩的機率,

                    $A\cup B$表至少有一小孩為男孩的機率, 

  故

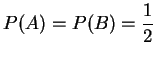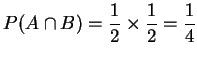         $P(A)=P(B)=\displaystyle \frac 12$, $P(A\cap B)=\displaystyle \frac 12\times \frac 12=\frac 14 $,

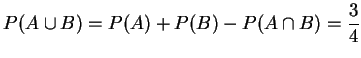         $P(A\cup B)=P(A)+P(B)-P(A\cap B)=\displaystyle \frac 34$。

因此

   (1) 已知老大為男孩, 老二為男孩的機率為

           。

    (2) 已知有一男孩之下, 兩個小孩均為男孩的機率為

          。

　

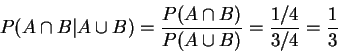隨堂練習1

投擲一公正的硬幣四次, 令表第一次為正面的事件, 表四次中至少出現三次正面的事件,

試求$P(B\vert A)$及$P(A\vert B)$。

[解]: $P(B\vert A)$=0.5, $P(A\vert B)$=0.8。

　

生活中的實例2

將$aabbcd$排成一列, 令表$b$排末的事件, 表兩個$a$相鄰的事件, 試求$P(B\vert A)$。
[解]:

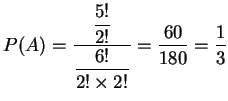      $\displaystyle P(A)=\frac {\displaystyle \frac {5!}{2!}}{\displaystyle \frac {6!}{2!\times 2!}}=\frac {60}{180}=\frac 13$,

因$A\cap B$表兩個$a$相鄰且$b$排末的事件, 所以

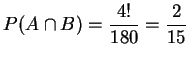     $\displaystyle P(A\cap B)=\frac {4!}{180}=\frac {2}{15}$, 

故

    

隨堂練習2

承實例2, 試求$P(A\vert B)$之值。

[解]:0.4。


生活中的實例3

甲生打算投擲一公正的銅板來決定要選修的課, 若出現正面則選修日文課, 若出

現反面則選修德文課。 從過去之資料得知選日文課有0.6的機率會得到90分以上, 

而選德文課只有0.4的機率會得到90分以上。 試求甲生選修日文課會得到90分以

上的機率為何?

[解]: 令

             表示選修日文課的事件,

            表示所選的課得到90分以上的事件, 所以

           $A\cap B$表選日文課得到90分以上的事件, 

 故

      =0.6×0.5=0.3。

 因此甲生選修日文課會得到90分以上的機率為0.3。

　

隨堂練習3

承實例3, 試求甲生選修德文課會得到90分以上的機率為何?

[解]:0.2。

　

生活中的實例4

袋中有紅球5個, 白球3個, 袋中有紅球3個, 白球2個, 先隨機地選出一袋, 再自選出的

袋中取出一球, 試求取出白球的機率。

[解]:

令W表取出白球, 則

\begin{eqnarray*} P(W)=P(A)P(W\vert A)+P(B)P(W\vert B)=\frac 12 \times \frac 38+\frac 12\times \frac 25=\frac {31}{80} \end{eqnarray*}

隨堂練習4

承實例4, 求取出的白球為來自袋的條件機率。

[解]:15/31。

  1. 衛生局至某大學免費檢驗某疾病, 此檢驗之可靠度為90%。 即若真有病, 則有0.9之機率

    呈正反應(假設檢驗只有正負反應); 若無病亦有0.05的機率呈正反應。 過去的資料顯示

    平均每100人有一人會有此病。此檢驗迅速且無害, 若檢驗呈正反應, 則"須"至醫院住院

    一週做進一步檢查。 試問你是否願意接受此檢驗?

    　

  2. 設甲, 乙二人在賭博, 甲投擲二公正銅板且不讓乙看到結果。此時丙從旁經過, 忍不住說

     他看見有一銅板朝上。甲聞言對丙說:你破壞了我們的賭局, 我的朋友乙正要猜兩個銅板

     朝上的面是相同還是相異。試問丙提供的資訊是否對乙有幫助?    

[解]: 

1. 不願意。

2. 有幫助。　

  1. 擲出兩顆骰子, 出現點數和為6時, 求其中一顆骰子為2點的機率

  2. 1-9號的卡片各一張, 從中任取2張發現點數和為偶數, 求此2張均為奇數的機率。

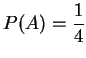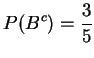  3. 設, 為樣本空間中的二事件, 若 $\displaystyle P(A)=\frac 14$, $\displaystyle P(B^c)=\frac 35$,

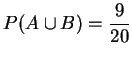    $P(A\cup B)=\displaystyle \frac {9}{20}$, 試求$P(B^c\vert A)$之值。

  4. 某生參加考試, 題目均為選擇題, 每題有5個選擇, 其中70%的題目該生

    會做答, 而對於不會的題目, 該生會任選一個答案

    (1) 求任一題目答對的機率。

    (2) 某一題答對, 求此題是猜中的機率。

  5. 投擲一公正的銅板10次, 且得到5個正面, 求下述二條件機率

    (1) 第一次得到正面。

    (2) 首五次恰得到3個正面。





[解答部分]

1. $\displaystyle \frac 25$。 

  2. $\displaystyle \frac 58$。   

3. $\displaystyle \frac 15$。   

4. (1) $\displaystyle \frac {19}{25}$, (2) $\displaystyle \frac {3}{38}$。   

5. (1) $\displaystyle \frac 12$, (2) $\displaystyle \frac {25}{63}$。