在伯努力試驗中，若每次成功的機率不一樣，則次試驗後，所得成功次數就不是二項分佈了。假設袋中有個球，其中有個白球，個非白球，自其中隨機地取出個球，每次取出後不放回(without replacement)。令表總共取得之白球數，則

。

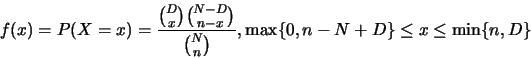則上式便定義出一超幾何分佈(hypergeometric distribution)，以表之，有三個參數。只要是取出後不放回，通常便引出超幾何分佈。因此諸如民意調查，及品質管制的討論裡常出現此分佈。

接下來我們說明之範圍的由來。因只取個球, 且白球數共只有個，所以不能超過及，即

。

又取中之非白球的個數當然不能超過全部之非白球數 ，即

，

而又要成立，因此

。

超幾何分佈的期望值與變異數分別如下:

。