常態分佈(normal distribution)又稱高斯分佈(Gaussian distribution)。德國的10馬克紙幣, 以高斯(Gauss, 1777-1855)為人像, 人像左側有一常態分佈之p.d.f.及其圖形。

高斯在數學上有諸多貢獻, 但在10馬克的紙幣, 挑出來與他相隨的, 是常態分佈。可見常態分佈不只在統計上, 在數學上亦很重要。不過高斯倒不是第一位提出此分佈者。法國數學家棣美弗(Abraham De Moivre, 1667-1754)早於他寫出此分佈。甚至一般認為丹尼爾•伯努力(Daniel Bernoulli, 1700-1782)更早就發現了。有人稱這種現象為誤稱定律(Law of Misnomer)。要知數學上的命名, 往往並非以實際發現者。

常態分佈之所以重要, 原因很多, 我們給出三個主要的原因:首先是常態分佈在分析上較易處理。
其次是常態分佈之p.d.f.的圖形為鐘形曲線(bell-shaped curve), 再加上對稱性, 使得很適合當做不少母體之機率模式。當然底下我們會看到鐘形且具對稱的分佈也有不少, 但通常不像常態分佈, 在分析上如此容易駕馭。第三個原因是由於在中央極限定理(Central Limit Theorem), 使得在不太強的條件下, 常態分佈可當做不少大樣本的近似分佈。

常態分佈有二參數μ及, , σ>0, 以表此分佈, p.d.f.為

μ稱為位置參數(location parameter), 此因μ影響圖形的位置, σ則為尺度參數, σ愈大表圖形散的愈開。底下給出三個有相同的μ, 但不同之p.d.f.的圖形, 以做比較。

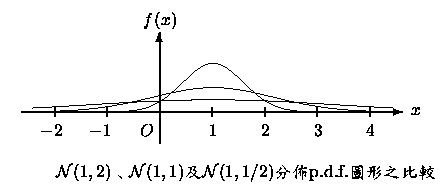
在 分佈裡, 二參數μ, , 分別為期望值與變異數, 即

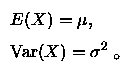
若X有分佈, 則

有分佈, 稱為標準常態(standard normal)分佈。其p.d.f.為

由X至Z的一變換稱為將X標準化, 分佈經標準化後, 便成為分佈。而標準常態分佈之期望值為0, 變異數為1。