在一組隨機樣本中, 有時候最大值、最小值或中間值,
是我們較有興趣的。例如, 過去五十年最大降雨量,
幾次跑步最短的時間, 台北市房價的中間值等, 這些都涉及順序統計量(order statistics)。
定義1.1 設
![]() 為一組隨機樣本, 按照小至大排出, 而得
為一組隨機樣本, 按照小至大排出, 而得
![]() , 便稱順序統計量。
, 便稱順序統計量。
順序統計量滿足
![]() 。特別地,
。特別地,
在美國, 職業球隊裡, 例如職棒 、職籃,
極少數的球員薪水(或收入)很高, 但大部分的球員薪水是很低的。
報紙上, 有時會刊出某位球員與球隊簽下新的合約, 五年薪水一億美元。
平均一年兩千萬美元, 尚不包括廣告等收入! 當球員抱怨薪水太低時,
老闆可能會想全隊平均年薪已有百萬美元了,
但球員會想有一半以上的球員年薪少於二十萬美元
(職業球員由於球齡短以及會因受傷而結束球員生涯,
所以薪水是較其他行業高)。這兩個觀點都是正確的, 只是一計算平均,
一計算中位數。當討論到收入、價格等含有一些較極端的值
(過高或過低), 中位數可能是一較合理的指標值。
若
![]() 為一由連續型的母體所產生之隨機樣本,
則任二隨機變數
為一由連續型的母體所產生之隨機樣本,
則任二隨機變數
![]() , 會相等的機率為 0,
因此
, 會相等的機率為 0,
因此
![]() 。
下述定理給出任一順序統計量之分佈。
。
下述定理給出任一順序統計量之分佈。
定理1.1 設
![]() 為由連續分佈函數
為由連續分佈函數![]() , 且p.d.f.為
, 且p.d.f.為![]() , 所產生之隨機樣本,
, 所產生之隨機樣本,
![]() 表其順序統計量。則
表其順序統計量。則![]() 之p.d.f.為
之p.d.f.為
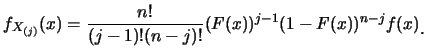 |
(1.1) |
| (1.2) | |||
 |
例1.1 設
![]() 為由
為由
![]() 分佈所產生隨機樣本。
則
分佈所產生隨機樣本。
則
![]() 。利用定理5.1, 得
。利用定理5.1, 得
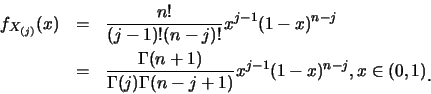
例1.2 設
![]() 為由分佈函數
為由分佈函數![]() 所產生之隨機樣本。
則
所產生之隨機樣本。
則
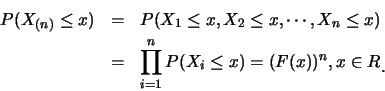
| (1.3) |
另外,
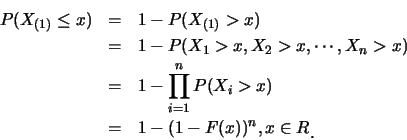
| (1.4) |
例如, 若
![]() 之共同分佈為
之共同分佈為
![]() ,
則由(5.4)式, 即得
,
則由(5.4)式, 即得
![]() ,
仍有指數分佈, 只是參數改為
,
仍有指數分佈, 只是參數改為![]() 。此為一有趣的結果。
。此為一有趣的結果。
定理1.2 設
![]() 為由連續分佈函數
為由連續分佈函數![]() , 且
p.d.f.為
, 且
p.d.f.為![]() , 所產生之隨機樣本,
, 所產生之隨機樣本,
![]() 表其順序統計量。則
表其順序統計量。則
![]() , 之聯合p.d.f.為
, 之聯合p.d.f.為
| (1.5) | |||
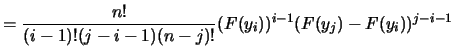 |
|||
上定理的證明我們略去了。三個或更多個順序統計量的聯合
p.d.f.亦可求出。如設整數
![]() , 則
, 則
![]() 之聯合p.d.f.為
之聯合p.d.f.為
| (1.6) | |||
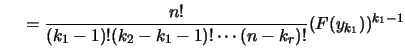 |
|||
| (1.7) | |||
在(5.7)式中, ![]() 的出現是很顯然的: 對任一組
的出現是很顯然的: 對任一組
![]() ,
有
,
有![]() 組
組
![]() , 其順序統計量均對應
, 其順序統計量均對應
![]() 。
。
底下給幾個例子。
例1.3 設![]() 為由p.d.f.
為由p.d.f.![]() ,
, ![]() ,
所產生之隨機樣本。則
,
所產生之隨機樣本。則
![]() 之聯合p.d.f.為
之聯合p.d.f.為
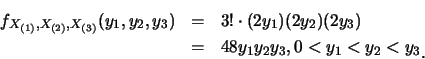
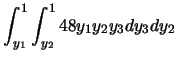 |
(1.8) | ||
 |
(1.9) | ||
例1.4 設
![]() 為由
為由
![]() 分佈所產生之隨機樣本。
令全距
分佈所產生之隨機樣本。
令全距
![]() , 半全距(midrange)
, 半全距(midrange)
![]() 。
試求
。
試求![]() 之聯合
之聯合
p.d.f., 邊際p.d.f., ![]() 及
及![]() 。
。
解.首先
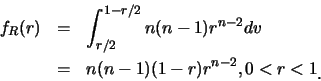
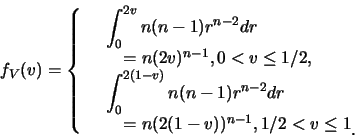
有了![]() 及
及![]() 之邊際p.d.f., 便可求出
之邊際p.d.f., 便可求出![]() 及
及![]() 。如
。如
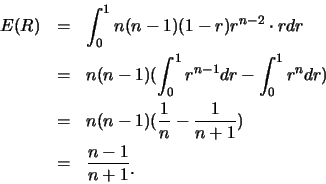
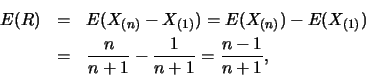
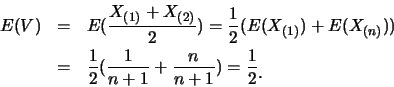
例1.5 某廠牌燈管宣稱可使用![]() 小時,
某辦公室最近安裝40支該廠牌的燈管, 才使用1個月便壞了一支。這是否合理呢?
小時,
某辦公室最近安裝40支該廠牌的燈管, 才使用1個月便壞了一支。這是否合理呢?
解.為了便於計算, 我們假設燈管的壽命有指數分佈。
即設燈管壽命
![]() 為i.i.d.之
為i.i.d.之
![]() 分佈,
期望值
分佈,
期望值
![]() (小時)。又設每月上班25天,
每天開燈10小時。
(小時)。又設每月上班25天,
每天開燈10小時。
對一特定的燈管, 使用1個月(250小時)內會壞的機率為
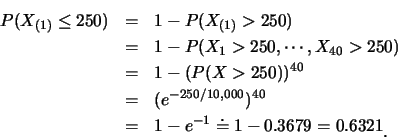
至於5個月(![]() 小時)內至少壞一支燈管的機率為
小時)內至少壞一支燈管的機率為
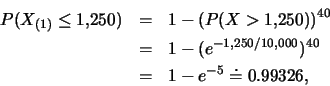
雖平均壽命為![]() 小時,
但至少有一燈管10年(
小時,
但至少有一燈管10年(![]() 小時)後仍可使用的機率有多大呢?
即要求最大順序統計量
小時)後仍可使用的機率有多大呢?
即要求最大順序統計量![]() 要大於
要大於![]() 之機率:
之機率:
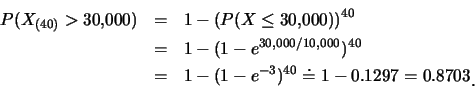
底下我們來看一些關於順序統計量之極限結果。
例1.6 設
![]() 為由
為由
![]() 分佈所產生之隨機樣本,
分佈所產生之隨機樣本,
![]() 。令
。令![]() ,
,
![]() 。
則對
。
則對
![]() ,
,
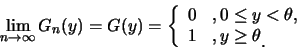
| (1.10) |
例1.7 設
![]() 為由p.d.f.
為由p.d.f.
![]() ,
, ![]() ,
所產生之隨機樣本,
,
所產生之隨機樣本,
![]() ,
, ![]() 。令
。令![]() ,
,
![]() 。則對
。則對![]() ,
,
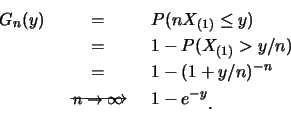
次令![]() 。則可證明
。則可證明
![]() , 其中
, 其中
![]() ,
, ![]() (習題第18題)。
(習題第18題)。