

![]()

在說明乘法原理之前, 我們首先考慮下述問題:
設有三名男生(甲、乙、丙)及三名女生(丁、戊、己)參加聯誼活動, 某遊戲需男女配對一同進行,
試問共有幾種不同的配對方式?
首先, 我們先將可能的配對方式一一列出:
甲丁、甲戊、甲己、乙丁、乙戊、乙己、丙丁、丙戊、丙己
可以發現共有9種配對方式。 但若人數太多, 一一列出可能很繁雜, 因此我們用另一方式來解這個
問題。 我們將此問題分成兩個步驟: 第一個步驟: 先從3名男生中選一名, 共有3種選法, 第二個步
驟由3名女生中選一名, 也有3種選法。因第一個步驟中每選一名男生, 都有3名女生可供選擇, 故共
有![]() 種選法。
種選法。
如果將上面配對過程看做完成某一件事的過程, 將選擇男生看做完成此事的第一個步驟,而完成
將選擇女生看做完成此事的第二步驟,
並且分別將3名男生, 與3名女生看成完成第一步有![]() 種方法,
種方法,
第二步有![]() 種方法,
則完成這件事共有
種方法,
則完成這件事共有![]() 種方法。
事實上, 我們可以推廣至更一般的形式,
種方法。
事實上, 我們可以推廣至更一般的形式,
即所謂的乘法原理。
有了乘法原理後,接下來我們看看下面問題:
假設某教室內有![]() 張椅子, 有
張椅子, 有![]() 位學生依序選擇座位,
試問共有幾種不同的選法?
位學生依序選擇座位,
試問共有幾種不同的選法?
解這個問題可分![]() 個步驟,
個步驟,
第一步:第一位學生先從![]() 張椅子任選一張, 共有
張椅子任選一張, 共有![]() 種選法,
種選法,
第二步:第二位學生從剩下的![]() 張椅子任選一張, 共有
張椅子任選一張, 共有![]() 種選法,
種選法,
第三步:第三位學生從剩下的![]() 張椅子任選一張, 共有
張椅子任選一張, 共有![]() 種選法,
種選法,
至第![]() 步:第
步:第![]() 只能剩下的2張椅子任選一張,
共有2種選法,
只能剩下的2張椅子任選一張,
共有2種選法,
至第![]() 步:第
步:第![]() 位學生只能選剩下的一張椅子,
故只有
位學生只能選剩下的一張椅子,
故只有![]() 種選法。
種選法。
由乘法原理知: 共有
![]() 種選法。
種選法。
我們通常會將
![]() 用
用![]() 來表示。讀做"
來表示。讀做"![]() 階乘"。
即
階乘"。
即
其中
![]() , 通常會將
, 通常會將![]() 定義為1。
定義為1。
底下是一些常用的階乘值。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
除了乘法原理外, 尚有一重要的加法原理:
例如, 從甲地到乙地有飛機、火車與巴士等三種交通工具可到達,其中飛機每天有3班, 火車每天
有15班, 巴士每天25班,若A先生欲從甲地至乙地, 很明顯地, 可看出此問題的A先生只能選擇一種交
通工具的某個班次, 故共有3+15+25=43個交通班次可選擇。
![]()
生活中的實例1
某兔穴有進出口四處, 一兔由不同一口進出的方法共有幾種?
[解]: 第一個步驟: 進→4種選法。
第二個步驟: 出→3種選法。
由乘法原理知, 共有![]() 種方法。
種方法。
生活中的實例2
假設某教室有四張椅子, 甲、乙、丙、丁四位學生依序選擇座位,
試問共有幾種不同的選法?
[解]:
第一步:
甲生從四張椅子任選一張![]() 4種選法;
4種選法;
第二步: 在甲生選定後,
乙生從剩下三張椅子任選一張![]() 3種選法;
3種選法;
第三步: 在甲乙二人選定後,
丙生從剩下二張椅子任選一張![]() 2種選法;
2種選法;
第四步: 在甲乙丙三人選定後,
丁生只能選擇剩下的一張椅子![]() 1種選法;
1種選法;
由乘法原理知, 共有
![]() 種選法。
種選法。
隨堂練習1
某速食店舉辦週年慶, 提供主餐5種, 副餐4種, 飲料6種, 任選主餐、副餐與飲料各一種, 特價70元,
試問顧客有多少種選擇的方式?
[解]: 120種。
隨堂練習2
甲、乙兩人在排成一列的8個座位中相鄰而坐, 試問共幾種不同的坐法?
[解]: 14種。
生活中的實例3
試求下列各值。
(1)
![]() , (2)
, (2)
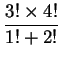 。
。
[解]:
(1) 原式
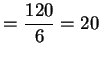 。
。
(2) 原式
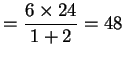 。
。
生活中的實例4
假設某期刊室內, 有5種週刊, 4種月刊, 3種季刊供民眾閱讀, 今甲生從這些期刊中任選一種,
試問共有幾種不同的選法。
[解]: 因總共期刊數有5+4+3=12種, 所以甲生從這12種中選一種, 故共有12種不同的選法。
隨堂練習3
試求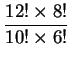 之值。
之值。
[解]: 7392
隨堂練習4
某校想了解學生對法律常識的認識, 想從該校高三有20班, 高二有19班, 高一有18班,任選一班進行
法律常識測驗, 試問共有幾種不同的選法?
[解]:57種。

位號碼由1至52號編排。 其中1號靠左窗, 2號靠右窗, 3號靠走道左側, 4號靠走道右側, 餘
此類推。今有甲、乙、丙三位學生分別購買一張火車票, 若三人皆坐在第二節車廂的同一行,
且甲生的座位號碼為42, 試問
(1) 此三人座位是靠左窗、靠右窗、靠走道左側還是靠走道右側?
(2) 此三人共有多少種不同的坐法?
(3) 若此三人前後緊鄰而坐, 有幾種不同的坐法?
(4) 若三人之座位號碼和為3的倍數, 共有多少種不同的坐法?
(5) 若三人之座位號碼和為90, 共有多少種不同的坐法?
小組(各三班),進行單淘汰比賽(每小組首輪有一班輪空),產生分組冠軍後, 4隊再進行單循
環比賽,以決定前四名名次。試問
(1) 共需安排多少場比賽?
(2) 若該校共有4個球場,每天只有二個時段能安排賽程, 且每班每天最多賽一場,則學校最
少需安排多少天的賽程?
[解答]
1.(1) 靠右窗, (2) 132種, (3) 2 種,(3) 46種, (4) 10種。
2. (1) 26場, (2) 6天。

(1) ![]() , (2)
, (2)
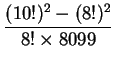 。
。
(1) 若二人上山可同路, 下山不同路, 則有幾種方法?
(2) 若兩人上山不同路, 下山亦不同路, 則有幾種方法?
(1) 若![]() 、
、![]() 、
、![]() 成等差數列, 則有幾種情形?
成等差數列, 則有幾種情形?
(2) 若![]() 、
、![]() 、
、![]() 成等比數列且公比為整數, 則有幾種情形?
成等比數列且公比為整數, 則有幾種情形?
的襪子, 則有幾種不同的放法?
若最後一位數字不能為4, 且後四位數字沒有0000這個號碼, 那麼該國可能有的自用小汽車
的牌照號碼有多少個?
最後一個(提示: 位數不超過3位)。
[解答]
1. (1) 40206, (2) 40320。
2. (1) 54, (2) 36。
3. 18。
4. (1) 27, (2) 3。
5. 6。
6. 8種。
7.
![]() 種。
種。
8. 145。