

![]()

機率的意義究竟是什麼?
在某些條件下我們稱一事件![]() 發生的機率為
發生的機率為![]() ,
此處的
,
此處的![]() 含義為何?
含義為何?
不同的書不同的作者, 往往有不同的定義方式, 但大致可分為下述三種:
(1) 將機率的概念以"相同的可能性"(equal possibility)來解釋, 此為古典的定義。
假設所有試驗結果之機率相等, 若有![]() 個試驗結果,
則平均分配機率
個試驗結果,
則平均分配機率![]() 至每一試驗結果。
至每一試驗結果。
就投擲一公正銅板的試驗而言, 認為兩種試驗結果(正面和反面)有相同的可能性是合理的,因此
分配每一試驗結果之機率為0.5, 即觀察到是正面的機率是0.5, 觀察到是反面的機率也是0.5。若
是投擲一公正骰子的試驗, 認為六種可能結果有相同的可能性也是合理, 因此分配每一試驗結果之
機率為1/6, 即出現1點的機率是1/6, 6點的機率也是1/6, 餘類推。
(2) 以多次重複試驗後, 一事件出現的頻率(frequency)來表示機率, 此即統計的定義, 或客觀的解釋。
由於古典的定義不夠一般性, 因它無法用來描述一有無限可能性的試驗結果。以頻率來解釋機率,
必須針對是可以重複做試驗的事件, 如丟銅板等。由於是實驗的結果, 與觀察者是誰無相關, 因此
又稱客觀的解釋。如某公司新產品試賣中, 接觸了400位顧客, 其中100位買該產品而300位沒買。事
實上, 可以想像每接觸一位顧客, 相當於做了一次試驗, 重複試驗了400次, 而當中有100次顧客
買該產品, 300次顧客沒有買, 因此我們可以說顧客購買該產品的機率為100/400=0.25。同理, 顧客
沒有買該產品的機率為300/400=0.75。
(3) 以觀察者對一事件的相信程度來定義機率, 此即主觀的觀點。
當試驗結果相同的可能性之假設不合理, 我們可以採用主觀的觀點。主觀的觀點是根據過去客
觀的事實來決定, 即使有相同的資料, 不同的人對同一事件, 有時也會給出不同的主觀機率。如考慮
中華台北對美國的世界盃棒球賽, 中華台北贏的機率是多少? 很顯然地, 比賽結果輸、贏的可能性不
相等。同時過去中華台北對美國的次數並不多, 因此若想估計中華台北獲勝的機率, 我們必須用主觀
的觀點, 如評量雙方的投手之防禦率, 或打擊者之打擊率等, 給予一個值以表示中華台北會贏的相信
程度。
當然無論使用那一種的機率的定義方式, 都需滿足下列條件:
(i) 給予每一試驗結果的機率必須介於0與1之間,
(ii) 全部試驗結果之機率和必須等於1
給予每一試驗結果之機率後, 我們就可以給出任何事件的機率。任何事件之機率等於該事件所有試驗
結果機率之和。如投擲一公正的骰子,
因出現每一點的機率都是1/6, 所以若令事件![]() 表出現點數為
表出現點數為
偶數的事件, 即![]() ={2,4,6},
則事件
={2,4,6},
則事件![]() 的機率為出現2點,
4點, 6點的試驗結果之機率加總, 即
的機率為出現2點,
4點, 6點的試驗結果之機率加總, 即
1/6+1/6+1/6=1/2, 通常以![]() 來表示事件
來表示事件![]() 之機率,
因此
之機率,
因此![]() =0.5。
=0.5。
關於機率有一些基本的性質, 我們列於下:
設![]() 、
、![]() 為樣本空間
為樣本空間![]() 中的二事件,
則
中的二事件,
則
(1) ![]() ,
,
![]() ,
,
(2) ![]() ,
,
(3) 餘事件的機率: ![]() ,
,
(4) 機率的加法性: ![]() ,
,
(5) 若![]() 、
、![]() 為互斥事件,
則
為互斥事件,
則![]() , 且
, 且 ![]() ,
,
(6) 單調性: 若![]() ,
則
,
則![]() 。
。
![]()
生活中的實例1
投擲一公正的銅板兩次, 試求出現兩個正面的機率。
[解]: 若以"正反", 表第一次出現正面, 第二次出現反面, 餘類推。因此樣本空間
![]() ={正正, 正反,
反反, 反正},
={正正, 正反,
反反, 反正},
我們可以認為這四種試驗結果有相同的可能性, 因此分配每一試驗結果的機率為1/4, 所以
出現兩個正面的機率為1/4。
隨堂練習1
投擲一公正的骰子兩次, 試求出現兩個3點的機率。
[解]: 1/36。
生活中的實例2
某一醫院X光部門, 連續30天記下早上九點鐘等待服務的病人人數, 得下列結果:
| 等待人數 | 發生的天數 |
| 0 | 5 |
| 1 | 7 |
| 2 | 10 |
| 3 | 5 |
| 4 | 3 |
試求等待人數為1的機率為何?
[解]: 我們可以假設每一天為一次試驗, 重複試驗了30次, 而等待人數為1, 共出現了7次, 所以機
率為7/30。
隨堂練習2
承實例2, 試求等待人數為2的機率。
[解]: 1/3。
生活中的實例3
甲先生和乙先生出價買一棟房子, 有兩種可能的結果:
![]() =他們出的價格被接受
=他們出的價格被接受
![]() =他們出的價錢被拒絕
=他們出的價錢被拒絕
甲先生相信他們出價被接受的機率是0.7,
因此甲先生設![]() =0.7。乙先生相信他們出價被接
=0.7。乙先生相信他們出價被接
受的機率為0.5, 因此乙先生設![]() =0.5。我們可以注意到乙先生在出價是否被接受上,
較甲
=0.5。我們可以注意到乙先生在出價是否被接受上,
較甲
先生悲觀。
隨堂練習3
承實例3, 在甲乙兩位個人主觀條件下, 分別求出他們認為出價被拒絕的機率。
[解]:甲先生相信他們出價被拒絕的機率是0.3; 乙先生相信他們出價被拒絕的機率是0.5。
生活中的實例4
一袋中有3個紅球, 4個白球, 5個黑球, 今自袋中任取3球, 試求取出3球為同色之機率。
[解]: 任取3球的可能結果共有![]() =220種,
所以出現每一種的機率均為1/220。因3球為同色,
=220種,
所以出現每一種的機率均為1/220。因3球為同色,
所以可能情形為: 3球皆為紅球有![]() =1種,
3球皆為白球有
=1種,
3球皆為白球有![]() =4種, 3球皆為黑球有
=4種, 3球皆為黑球有![]() =10種,
=10種,
故共有15種。因每一種機率皆為1/220, 所以15種之機率為15/220=3/44, 即取出3球為同色之機
率為3/44。
隨堂練習4
承實例4, 試求取出3球為不同顏色的機率。
[解]: 3/11。
生活中的實例5
設![]() 與
與![]() 為樣本空間
為樣本空間![]() 中之二事件,
且已知
中之二事件,
且已知![]() =0.3,
=0.3,
![]() =0.4,
=0.4, ![]() =0.1,
試求
=0.1,
試求
(1) ![]() ,
(2)
,
(2) ![]() 。
。
[解]:
(1) ![]() =0.3+0.4-0.1=0.6。
=0.3+0.4-0.1=0.6。
(2) ![]() =0.4-0.1=0.3
=0.4-0.1=0.3
隨堂練習5
在某一研究發現有30%家庭的先生和20%家庭的太太會定時收看星期日晚上的某一節目。有12%的家
庭是夫婦同時收視此節目。試求夫婦中至少有一人會定時收視此節目之機率是多少?
[解]: 0.38

略去)與次數統計如下表:
| 層級 | 2級 | 3級 | 4級 | 5級 | 6級 |
| 次數 | 30 | 30 | 20 | 15 | 5 |
依此數據推測下述問題
(1) 餘震小於4級的機率。
(2) 餘震不小於5級的機率。
(3) 連續兩次平均餘震為4級的機率。
在上學途中會遇到紅燈的次數與機率如下:
| 次數 | 0 | 1 | 2 | 3 | 4 | 5 |
| 機率 | 0.05 | 0.15 | 0.20 | 0.20 | 0.10 |
依此數據試求下述問題:
(1) ![]() 之值,
之值,
(2) 遇到紅燈在四次以上的天數,
(3) 遇到三次以上紅燈之機率,
(4) 遇到兩次以下紅燈之機率。
[解]
1. (1) 0.5, (2) 0.2, (3) 0.16。
2. (1) 0.30, (2) 6天 (3) 0.6, (4) 0.4。

的機率為何?
(1) 三顆點數均相異,
(2) 三顆點數均相同,
(3) 出現點數和為8,
(4) 出現點數和為15。
(1) 任取兩張, 一紅一黑,
(2) 任取兩張, 不同號碼,
(3) 任取五張, 同花色。
(1) 恰好出現1點三次,
(2) 至少出現1點三次。
買到的機率是0.3。 試問兩人皆未買到對號火車票的機率為何?
[解答部分]
1.
![]() 。
。
2. (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
![]() , (4)
, (4)
![]() 。
。
3. (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
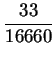 。
。
4. (1)
![]() , (2)
, (2)
![]() 。
。
5. ![]() 。
。