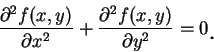前　　言

  a

        微分方程式分為兩類: 原微分方程式 (或稱常微分方程式, 簡稱 ODE), 及偏微分方程式 (簡稱 PDE)。簡單地講, 一未知的量為函數的方程式中, 若含有導數, 便稱為微分方程式。而解微分方程式, 便是將方程式中未知的函數解出。而若一微分方程式中的未知函數為單變數, 便稱為原微分方程式; 若未知函數為多變數, 便稱為偏微分方程式。

　　例如,

\begin{displaymath} f'(x)=f(x), \end{displaymath}

(1.1)

為一簡單的原微分方程式。顯然 $f(x)=e^x$ 為一解。稍後我們會看到, 任一滿足 (1.1) 之解必有 $f(x)=Ce^x$ 的形式, 其中 $C$ 為一常數。又如若 $f'(x)=g(x)$, 則 $f(x)=\int g(x)dx+C$, 即 $f$ 為 $g$ 之一反導數。故求反導數亦可視為解一微分方程式。

　　另外, 下式為一簡單的偏微分方程式:

\begin{displaymath} \frac {\partial ^2 f(x,y)}{\partial x^2}+\frac {\partial ^2 f(x,y)}{\partial y^2}=0\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(1.2)

此為一種 Laplace 方程式, 產生自電學、磁學、 流體力學及一些其他的領域中。(1.2) 式有許多不同形式的解, 如$f(x,y)=ax+by$ , 其中$a$ , $b$ 為二常數, $f(x,y)=e^x\cos y$及$f(x,y)=\log(x^2+y^2)$等。

　　在工程及科學中的許多應用性的問題, 往往可以化為一解微分方程式的問題。自十七世紀起, 牛頓、 萊布尼茲及 Johann Berneulli, 解一些產生自幾何學及機械中的簡單的微分方程式, 開啟了微分方程式的探討。此約始自西元 1690 年的早期探討, 令那時的數學家, 以為所有產生自幾何及物理中的微分方程式的解, 皆可以微積分中常見 的初等函數來表示。因此早期的工作, 都是試圖以初等的方法 , 發展一些解微分方程式的技巧。

　　一些特殊的解微分方程式的方法, 如分離變數, 及利用積分因子, 差不多可以說是在十七世紀結束前, 偶然之間產生的。在十八世紀, 主要歸功於歐拉、Lagrange 及 Laplace, 發展出更有系統的解微分方程式的步驟。而很快地數學家發現, 只有極少數的微分方程式, 可以初等的方法解出。逐漸地, 數學家也了解, 要找出能解出所有微分方程式的方法, 乃屬不可能。取而代之的是, 他們發現一微分方程式是否有解, 以及若有解的話, 由所給的微分方程式導出其解的性質, 這其中有更多值得探討的題材。 在此架構下, 數學家開始將微分方程式視為產生新函數的來源。

　　在一微分方程式中, 我們常以 $y$ 表示函數$f(x)$, $y'$ 表函數 $f'(x)$, 一般而言以 $y^{(n)}$ 表 $f^{(n)}(x)$。當然也可不用 $y$ 而用 $u$, $v$, $z$ 等。若 $G$ 為一 $(n+2)$ 個變數的函數, 則

\begin{displaymath} G(x, y,y',y'',\cdots,y^{(n)})=0, \end{displaymath}

(1.3)

便稱為一 $n$ 階之常微分方程式。即一微分方程式中所出現導數之最高階者, 即為該微分方程式之階。例如, $y'=y$ 及 $y'=x^3y+\sin(xy'')$ 分別為 一階及二階之微分方程式。而最高階導數之最高乘冪, 稱為該微分方程式之次數 。例如, $1+(y')^2=(y+xy')^2$ 及 $(1+(y')^2)^3=3(y'')^3$ 分別為二次一階, 及三次二階 微分方程式。就微分方程式之本質而言, 通常次數之重要性較小, 因此我們往往只提其階數。一函數 $f$, 若滿足對每一屬於 $f$ 定義域中的 $x$,

\begin{displaymath} G(x, f(x),f'(x),f''(x),\cdots,f^{(n)}(x))=0, \end{displaymath}

則稱為 (1.3) 之一解。

　　在西元 1820 年左右, 柯西得到第一個關於微分方程式解之存在性定理 。他證明對每一有下述形式之一階方程式:

\begin{displaymath} y'=f(x,y), \end{displaymath}

只要 $f(x, y)$ 滿足某些一般的條件, 便有一解存在。其中一個重要的例子是 Ricatti 方程式 :

\begin{displaymath} y'+P(x)y+Q(x)y^2=R(x), \end{displaymath}

(1.4)

其中 $P$、$Q$ 及 $R$ 為給定之函數。柯西的結果導至對 $\forall r>0$, 只要 $P$、$Q$ 及 $R$ 在 $(-r,r)$ 中, 有冪級數展式, 則 (1.4) 式在 $(-r,r)$ 中有解。在西元 1841 年, Liouville 證明在某些情況下, (1.4) 之解無法以初等函數表示出。

　　本章只是對常微分方程式做一初步的介紹, 給出一些基本的結果。進一步關於微分方程式的討論, 可見其他專門的書籍。

　　首先, 對微分方程式

\begin{displaymath} y'=2, \end{displaymath}

(1.5)

易見

\begin{displaymath} y=2x+C \end{displaymath}

(1.6)

為其解, 其中 $C$ 為解之參數。而任一 (1.5) 之解必有 (1.6) 的形式。(1.6) 式便稱為 (1.5) 之一般解 。(1.6) 所給出的解為平面上所有斜率為 2 之直線。這些直線即為一曲線族 。同理

\begin{displaymath} xy'+y=0 \end{displaymath}

之一般解為

\begin{displaymath} xy=C, \end{displaymath}

此為平面上以二座標軸為漸近線之雙區線所形成之一曲線族, $C$ 為其參數。

　　反之, 通常一具有一個參數之曲線族, 往往也會是一階微分方程式的一般解。例如,

\begin{displaymath} y=Cx^2, \end{displaymath}

(1.7)

描述出一以 (0,0) 為頂點, $y$ 軸為中心之拋物線族。將 (1.7) 左、 右分別對 $x$ 微分, 得

\begin{displaymath} y'=2Cx\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(1.8)

由 (1.7) 及 (1.8) 消去 $C$, 即得

\begin{displaymath} xy'=2y\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

(1.9)

可證明 (1.7) 為 (1.9) 之一般解, 因此 (1.9) 便完全描述出拋物線族 (1.7)。

例 1.求一描述雙曲線族

\begin{displaymath} xy=Cx-1 \end{displaymath}

(1.10)

之微分方程式。　　

　

　　其次我們介紹起始條件。首先可證明微分方程式

\begin{displaymath} x+yy'=0 \end{displaymath}

之一般解為同心圓

\begin{displaymath} x^2+y^2=C\mbox{\raisebox{-1.2mm}{\large . }} \end{displaymath}

若給定平面上一點, 則恰有一圓通過過此點。圓 $x^2+y^2=2$ 稱為 $x+yy'=0$ 之 一特別解 , 此為通過 $x=1$, $y=1$ 之唯一解。這種 $x=1$ 時, $y=2$ 稱為一微分方程式之起始條件。

　　一個一階之微分方程式, 其一般解中只有一參數, 故一起始條件便足以決定一特別解。若有一二階微分方程式, 便需二起始條件才能決定一特別解。高階微分方程式可類推。
　　

進一步閱讀資料：黃文璋(2002). 微分方程式。微積分講義第十一章，國立高雄大學應用數學系。